前節の書き出しで説明した座標系の定義を代数的に表すには、3次元の幾何学では四つのベクトルの一組を使います。これは、座標軸の単位長さと向きとを指示する三つの単位ベクトルa、b、cと、原点の場所を示す一つの位置ベクトルd とです。ベクトルa、b、c は右手系の単位ベクトルで、互いに直交です。これら四つのベクトルを縦ベクトルの成分とした3×4の行列(マトリックス)M=(a, b, c, d) を、座標系を表す一つの数学量と約束します。座標系は下のように表記します。ただし、ベクトルや行列の記号の書き方にも数学の決まりがありますが、付録Aにまとめておきました。
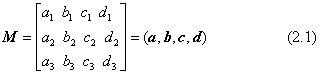
上の表記法を使って世界座標系自分自身を表すと下のようになります。
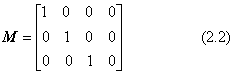
平面幾何の座標系の定義は、上の3次元の表現方法そのままで一つの軸の成分を使わないままにしておくか、または一つの軸の成分を省いて2×3の行列にまとめた形を使います。平面図形の幾何モデルを扱うときには、図形の奥行きを考えて、図を手前に出したり後ろに隠したりしますので、3×4の行列のままで使うことがあります。座標系を3×4や2×3の矩形行列で定義するのは、座標計算を形式的にベクトルと行列の演算で扱うことができるからです。幾何モデルの各部の座標が局所座標で表されているとき、これを世界座標系での座標値に変換させるのは、形式的に座標系の行列と局所座標を表す位置ベクトルとの積で計算します。したがって、「座標系の行列」は、「変換行列」の性質を持っています。座標系の行列と変換行列とは形式的に同じで、演算の約束も同じですが、その成分ベクトルの性質に違いがあります。それは、上の式のベクトルa、b、cの性質にあります。座標系の場合には「座標軸の直交性・右手系の関係・単位長さの定義」が成り立ちますが、変形を伴う変換ではこの定義が成り立たなくなります。
ベクトルや行列を数学的な記号式で表すのは、抽象的な議論をするときには便利ですが、コンピュータを使って具体的に数値計算をさせようというときには、二種類の知識が必要になります。第一は、コンピュータ内部で数値の表現に整数型と実数型とがあり、座標を数値で表すとき、数値が取り得る実用的な精度の関係で、世界座標が有限の範囲に制限されることです。第二は、数学記号を使った式と、コンピュータ言語を使った表現との相違を理解しておくことです。通常のコンピュータ言語では、ベクトルと行列とは配列を宣言して定義します。ベクトルは1次元の並びですが、行列は2次元の並びですので、メモリーの中では1次元の並びに直して記憶させます。この並べ方の約束がFORTRANとC/C++とで異なっています。FORTRANの2次元配列の定義は、行列を縦ベクトルの集合としますが、C/C++では行ベクトルの順に並べます。この相違は、FORTRANが数学式を扱う考えで設計されたコンピュータ言語であるのに対して、C/C++は文字列の集合を主に考えていることの相違からきています。
次のページ