6.3　蔓巻らせん

　平面内の曲線を扱う限りにおいては、前の節で説明した捩率ρが常に0になりますので、フルネ・セレの公式の出番がありませんが、三次元的な曲線では重要な性質を導くことができます。その例として、比較的眼に触れる機会の多い蔓巻螺旋の性質を示しましょう。円柱に紙テープをやや斜めにして巻き付けると、テープの縁の線がきれいな蔓巻き螺旋を描きます。構造物では、螺旋階段の手すりの曲線が典型的な蔓巻き螺旋です。ワイヤロープなどは撚りが複雑になっていますが、螺旋が複雑に組み合わさっています。自然界では朝顔のつるの巻き付きがそうです。

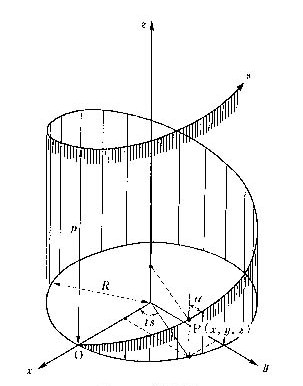
　図6.2で、朝顔の蔓のような巻き付けを俗に左回りといいますが、幾何学的には右ネジの溝の軌跡ですので右回りと呼びます。ワイヤロープでは素線の撚りの向きを区別するため、S撚りとZ撚りの呼び名が使われます。これは、素線を横から見たときの傾きを、SとZの字形の斜めの線の向きに当てはめた呼び名です。ちなみに、図6.2はZ撚りです。このように空間曲線では向きの定義には注意が必要です。図6.2のらせん曲線の座標を下のように与えます。

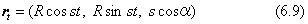
ただし、tは曲線を基準点Oから曲線に沿って測った長さ、αは円柱表面で曲線と円柱のz軸とのなす角度でピッチ角といいます。αは、撚りが左回りであれば負の値にします。定数sは次のように決まります。

　接線ベクトル、法線ベクトル、陪法線ベクトル、曲率、捩率は下のように求まります。

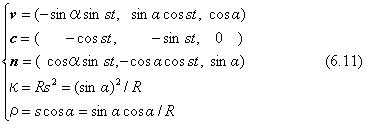
　螺旋が円柱を一周するときのz方向の高さを螺旋のピッチといいます。ピッチpは下のように計算されます。

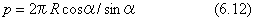
　空間曲線の例に蔓巻きらせんを挙げたのは、幾何学的な曲線の形状と針金のような材料を使った場合の曲線との微妙な違いを示したいためです。円柱に針金を巻き付けると、針金は曲率κで曲げられて円柱に接します。針金断面をz軸の方から見れば、針金断面が回転して見えますが、これが曲線の幾何学的な性質としての自然の捩じれです。しかし、この捩じれは、らせんの回転とは同期しなくて、円柱に接する針金断面の位置が次第にずれていきます。もし、地球を回る月がいつも同じ面を向くように、円柱に対して針金断面が同じ向きになるようにするには、針金を強制的に捩り込まなければなりません。針金の断面が丸いと気が付きにくいのですが、細い角柱を円柱に巻き付けようとすると、この無理が露呈します。紙テープを円柱に巻き付けるときは、紙テープに斜めの折れ線を付け、その折れ線を円柱の軸に平行にします。斜めに折るということが、曲げと同時に捩じれを加えていることになるのです。

　曲線を含む造形設計では、曲線としての幾何学的な曲げと捩じれと、断面自身が最初から曲がっていたり捩じれたりしている素材と、力を加わえて曲がったり捩じれたりすること、の三つが絡み合います。この面倒さを避けるため、曲線と言えば平面曲線の解析に重点が置かれます。曲面は二方向の曲線の組み合わせと考えることができますので、立体的な曲線だけの解析は流行らないようです。この章では曲面については触れません。その代わり、曲面を計算する簡単な内挿式を付録Ｇに付けてあります。