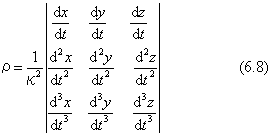三次元の世界座標に滑らかな曲線を考えます(図6.1)。点の座標を位置ベクトルで考えることにします。

曲線上に一つの基準点を決め、その点から曲線に沿って測った長さtをパラメータとして曲線上の点の位置を表すとします。
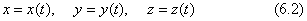
図6.1 空間曲線
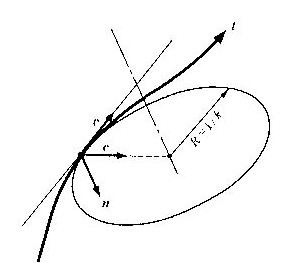
解析的に空間曲線を表す式には種々の形があります。式(6.2)の三つの式からパラメータのtを消去して二つの式、例えばf(x,y,z)=0、g(x,y,z)=0の形で考えることもあります。平面曲線の場合には、f(x,y)=0の形が曲線の一般式になります。いま、曲線上に近接した2点を考え、その座標をrおよびr+Δrとします。微小線分Δrのベクトル成分は、
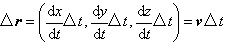
ここでvを曲線のt点での接線ベクトルといい、単位ベクトルです。
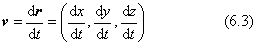
接線ベクトルvの成分をさらにtで微分して得られるベクトルを次の形で与えます。
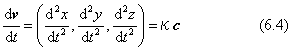
cを単位ベクトルに選び、スカラーκを下のように計算します。
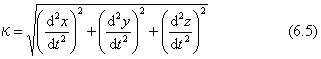
κをこの点での曲線の曲率、ベクトルcをこの曲線の法線ベクトルといいます。κの逆数1/κは、この点で曲線に接する円の半径(曲率半径)になります。法線ベクトルcは、円の中心を向きます(κとcとの符号をそれぞれ逆に定義することもできますが、向きの約束の違いはさし当たって問題にはなりません)。接線ベクトルvと法線ベクトルcとは直交する単位ベクトルです。この二つのベクトルと直交し、v、c、nが右手系の関係になるような三番目の単位ベクトルnを決め、これを陪法線ベクトルと定めます。
三つの単位ベクトルv、c、nを右手系の関係に定義付けをしましたが、これは次の三つのベクトル積を成り立たせています。
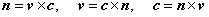
上の各式の両辺をそれぞれtについて微分した形を考えます。
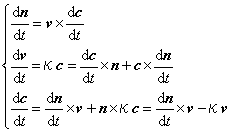
これら三つの微分式を同時に満足させる条件を求めると、新しい係数ρを使った下のような関係が得られます。
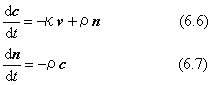
ここで導いた式(6.6)、(6.7)と先の曲率の式(6.4)とを加えた三つをフルネ・セレ(Frenet-Seret)の公式といい、曲線の解析に極めて重要なものです。ここで現れた係数ρは、陪法線もしくは法線の方向が接線の向きを軸として右回りに回転変化をする割合を与えますので、ねじれ率(捩率)といいます。スカラーρの値は下の行列式で求めます。