スプライン曲線の問題は、コンピュータグラフィックスに応用される前には、xの不等間隔で与えられたyの座標値からxの等間隔でのy座標値に切り直すというような、観測値や測定値のデータ処理に使われていました。もとのデータを生で繋ぐとごつごつした多角形になりますので、滑らかな曲線に近似できるように途中の座標値を補い、それを次のデータ処理に使います。そのため、この処理を曲線内挿または曲線補間と呼んでいました。これは実践的な技術ですので、なるべく簡単な数学理論を応用し、高級に見える理論に振り回されないような注意が必要です。
図6.6 曲線あてはめによる内挿例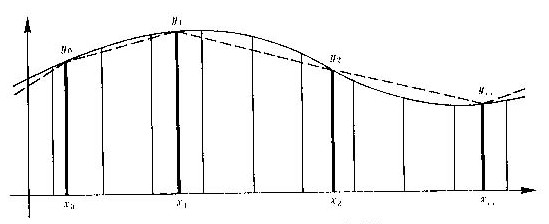
二次元の(x,y)座標において、xの昇順に(n+1)個の座標x0、x1、x2、…、xnを考え、それらの位置のyの座標値をy0、y1、y2、…、ynとします。この(n+1)個の点を結ぶような滑らかな関数y=f(x)を決めようという問題が、スプライン曲線理論の原点です。結論から言うと、関数f(x)を代数的なxのn次式一つで表すことは実用になりません。スプラインは、x座標のn個の区間ごとに独立な三次式を当て、接続箇所で左右の曲線のy、dy/dx、d2y/dx2の三つの値が等しくなるような連続条件を使う実践的な三次曲線です。そのため、三次のスプラインとも言います。実際の製図作業でも、幾つかの曲線定規を選んで、連続した3ないし4点を結ぶように曲線を描くものです(図6.6)。
代数学の問題としての三次方程式は、四つの係数(a,b,c,d)を持って、
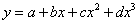
の形をしていますから、n個の区間ごとに三次方程式を定めるには4n個の未知係数を決める必要があります。区間ごとに両端の高さyが与えられていますから、必要な条件の数は2n個残ります。区間の接続箇所が(n-1)個あって、左右の曲線のdy/dxとd2y/dx2が等しくなるような条件を入れると、まだ二つの条件が不足します。そこで、通常は、全体区間の両端点でd2y/dx2=0の条件を加えます。
スプライン曲線を代数学的に解くだけならば味気のない問題ですが、これは構造力学では「三連モーメントの式」の応用として知られている生きた問題になります。それは、高さが不揃いな(n+1)個の支点で支えられた連続した弾性梁の変形を解析する問題になるからです。梁を支点の上で仮に切断して考えると、梁の形状は支点で折れ曲がった多角形になります。折れ曲がりを元に戻すように支点で梁に曲げモーメントを作用させて梁を変形させます。その変形は上の式と同じく三次式になります。支点の上で左右の曲げモーメントの大きさが同じになる条件が、上のd2y/dx2の連続条件に相当します。そして支点上での曲げモーメントを求める連立方程式が、連続梁における三連モーメント式として知られているものです。連続梁の両端では梁の曲げモーメントが0ですが、これが上のd2y/dx2=0の条件となります。
図6.7 隣接する辺の接続条件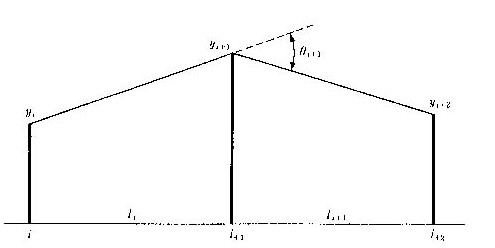
式の誘導などの細かい説明は省いて、計算に必要な基本の式だけを示しておきましょう。連続した3つの支点番号を(i-1)、i、(i+1)とします。支点のx座標に代えて、2径間の間隔をsi、si+1で与えます。支点の高さはyi-1、yi、yi+1、支点上での梁の曲げモーメントをki-1、ki、ki+1とします(図6.7)。梁の曲げ剛性は、変形計算の誘導では結果的に消去されてしまいますので、仮に単位の大きさとします。そうすると、曲げモーメントkは梁の曲率、つまりd2y/dx2と同じものです。支点上で梁の連続を断つと、支点iの上で左右の梁が折れ曲がります。その角度は、方向余弦の成分で下のようになります。
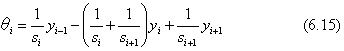
この角度が生じるように支点で梁に曲げモーメントkを作用させます。
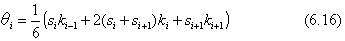
式(6.16)で、支点番号を1 … (n-1)と選ぶと曲げモーメントkに関する(n-1)元連立一次方程式が得られます。支点の数が(n+1)個ありますが、連続梁の両端ではk=0を代入します。この式(6.16)を行列の形に表すと、対角線要素とその両隣の要素だけに係数が並び、残りが0となる対称行列が得られます。いま、支点が等間隔であるとき、この行列の係数は下のようなきれいな帯行列(band matrix)の形になります。

式(6.16)の連立方程式は、次元数(n-1)が大きくても、消去法を使って簡単に数値計算ができます。kが計算できますと、支点i、i+1の区間の梁の変形を下の三次式で計算します。
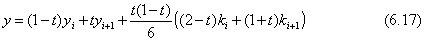
ただし、tは区間のx座標を無次元化して(0,1)で表したものです。
図6.8 平面図形のスプライン曲線
10 REM === Example Program of Spline Smoothing
20 DEF2PT P : DEF2ED E
30 INPUT "Number of Supports N(>2)=";N
40 XS=0.5*N+0.5 : YS=0.5 : WD=N-0.5 : DPWIND XS,YS,WD : CLS
50 DIM X(N),Y(N),Z(N),W(N)
60 FOR I=1 TO N : X(I)=I : Y(I)=RND(I) : LET PP=X(I),Y(I)
70 IF I<>1 THEN E=P0 @ PP
80 P0=PP :NEXT I
90 REM --- SOLVE ELASTIC EQUATION OF CONTINUOUS BEAM ----
100 Z(1)=0 : Z(N)=0 : W(N)=0
110 FOR I=1 TO N-2 : J=N-I
120 H1=X(J)-X(J-1) : H2=X(J+1)-X(J) : C1=H2/(H1+H2) : C2=1-C1
130 CD=(-C1*Y(J-1)+Y(J)-C2*Y(J+1))/(H1*H2)
140 CE=1.0/(2.0-C1*W(J+1))
150 Z(J)=(CD-C1*Z(J+1)*CE : W(J)=C2*CE : NEXT I
160 FOR I=1 TO N-2
170 Z(I+1)=Z(I+1)-W(I+1)*Z(I) : NEXT I
180 REM ---- DRAWS CONINUOUS CURVE ----
190 LET PP=X(1),Y(1)
200 FOR I=1 TO N-1 : H1=X(I+1)-X(I)
210 FOR T1=0.1 TO 0.91 STEP 0.1 : T2-1-T1
220 XS=X(I)+T1*H1 : YS=Y(I)*T2+Y(I+1)*T1
230 YS=YS+(Z(I)*(1.0+T2)+Z(I+1)*(1.0+T1))*T1*T2*H1*H1
240 P0=PP : LET PP=XS,YS : E=P0 @ PP
250 NEXT T1 : P0=PP : LET PP=X(I+1),Y(I+1) : E=P0 @ PP
260 NEXT I : M=M+1 : IF M<10 THEN CLS : GOTO 60
270 END