前の節で説明した曲線当てはめの式は、梁の変形理論に基づいていますが、そこでは一つの大きな条件を仮定しています。それは、梁がほぼ水平で、変形が小さいと仮定していることです。変形は二次元の(x,y)座標を使った関数y=f(x)のグラフを考えたからです。支点の上で切断した左右の梁の傾きは、角度の代わりに方向余弦の成分を使っています。コンピュータグラフィックスで、大きく曲がる曲線を扱う場合には、弾性梁の理論を拡張して3次のベジエ曲線を応用すると、曲線が不自然に見えません。その曲線とは、式(6.17)を下のようにベクトルの一次形式で表現したベジエ曲線を使うことです。
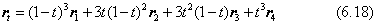
式(6.17)と式(6.18)とは随分違う形をしていますが、本質的に同じ曲線を表すものです。ここでは、(xi,yi)と(xi+1、yi+1)の支点座標をベクトルr1とr4とで置き換え、曲げモーメントによる変形の項を二つの中間制御点の座標r2、r3で書き換えてあります。r2、r3とは、支点での梁の接線方向を決定しますが、その位置は二つの支点r1とr 4との間を3等分するようにします。この3等分というのが梁の理論をモデル化する上でのノウハウになります。式(6.18)のようにベクトルの式で表すと、平面曲線だけでなく、空間曲線も表現できて、空間曲線の投影図を描く場合にも応用できます。
一般に、四つある制御点r0,r1,r 2,r3を順に通る滑らかな曲線を作りたいときは、下のようなベクトルの式を考えるのが実用的です。
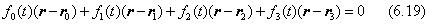
ここでfi(t)は、区間(0,1)で定義した無次元のパラメータtの3次関数とします。これらの関数は、t=0.33iの場所で、fi(0.33i)=1となる以外はすべて0 になるように決めればよいことになります。この方法をラグランジュ補間(Lagrange interpolation)といいます。ラグランジュ補間は、制御点の数(次数)が大きくなっても計算式を求めることができますが、4次式以上に応用することはあまりありません。この曲線あてはめと、3次のベジエ曲線とを含めた曲線の実用式を付録Gにまとめておきました。
次のページ