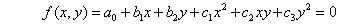
のように六個の係数を必要とする。曲線を描く場合には、曲線の座標をベクトルの一次形式で表すように整理し、データとして三点の座標を与える。描き始めの点r1と描き終わりの点r3を決め、もう一点r2を中間制御点とした三点のデータを与えれば二次曲線が描けるようにする。制御点の条件として、二次曲線では二つの場合を示した。一つは、t=1/2でr2を通り、そのときの接線がr1→r3の直線に平行である場合。もう一つは三角形r1, r2, r3に接する場合である。
いくつかの点の座標がデータとして与えられていて、それらを滑らかに結ぶような曲線を作り、中間の座標を求めたい。その式を曲線の内挿式という。内挿式の主な目的は、コンピュータ・グラフィックスで曲線を描く場合に応用する。曲線の座標は、t=0で描き始めの点を出発し、t=1で描き終わりの点に達するような無次元の曲線座標tを使う。ただし、tは曲線の長さには比例しない。曲線の座標はパラメータtを使った2次式または3次式を利用する。曲面の内挿は、曲線内挿を二方向に組み合わせた形で応用する。ここでは、縦横二方向に2次または3次の曲線を使うような部分的な曲面の内挿式を示す。
まず、二次曲線とは、放物線・円・楕円・双曲線をまとめていう。二次曲線の一般式は、平面座標(x,y)の二次形式で表され、
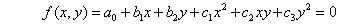
のように六個の係数を必要とする。曲線を描く場合には、曲線の座標をベクトルの一次形式で表すように整理し、データとして三点の座標を与える。描き始めの点r1と描き終わりの点r3を決め、もう一点r2を中間制御点とした三点のデータを与えれば二次曲線が描けるようにする。制御点の条件として、二次曲線では二つの場合を示した。一つは、t=1/2でr2を通り、そのときの接線がr1→r3の直線に平行である場合。もう一つは三角形r1,
r2, r3に接する場合である。
二次曲線の内挿式は、放物線・円・楕円・双曲線の種類に関わらず一つの式で表すことができて、曲線の種類は、たった一つのパラメータaの値を変えることで対応させることができる。比較的利用度の高いのは、三角形に内接する1/4楕円を描かせる場合である。データとして与える3つの頂点は、平行四辺形の1/4を作図するように決める。データとして直角二等辺三角形を与えれば、1/4円を描くことができる。
三次曲線の内挿式は、平面曲線だけでなく、一般的に空間曲線に応用することができる。この場合、始点と終点の他に中間制御点を2点使用する。内挿の場合には、4点を滑らかに結ぶ場合以外に、隣接する別の曲線と接線方向を合わせたい場合がある。この場合には、始点または終点に近い側の制御点は、接線方向を決める目的に利用する。中間制御点の選び方で、四種類の三次曲線の計算式を示した。このうち、始点と終点とでともに曲線の接線方向を決めるように中間制御点を利用する式は、3次のベジエ曲線である。なお、始点および終点で隣接する曲線と曲率まで連続させるようにした曲線の全体をスプラインと呼ぶ。
曲面を表す場合には、曲面を縦横2方向にu,vで考える曲線座標を使う。この座標はパラメータ座標であって、それぞれ区間[0,1]で定義する。この曲線座標は、曲面に沿って考えるが、長さには比例しない。曲面の内挿に使う基準点は、四辺形の四隅の点、または三角形の三頂点に加えて、中間の制御点である。制御点を識別するために、二つの整数番号i,jを使い、基準点の座標を位置ベクトルrijのように表す。曲面の内挿式の一般形は次のように表す。
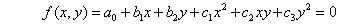
係数kijの表式は、u,vの関数として表にまとめた。なお、ここで表した内挿式は、中間の制御点が、u,vの座標値で、(0, 1/2, 1)または(0, 1/3, 2/3, 1)のときに一致する、という条件で表してある。