第３章　幾何学的要素の代数的な表し方

3.1　図形の性質を持たせた幾何学的要素

　基本的な幾何学的要素の点(point)・直線(line)・面(plane)は、非常に抽象的な概念です。サイコロのような具体的な形状を例にして正六面体を説明するときには、図形要素として頂点(vertex)・辺 (edge)・表面(face)の用語が使われます。頂点・辺・表面は、幾何学的要素の点・直線・面の性質がありますが、これらと同じものではありません。この区別を英語に例えると、図形要素は物と考えることができて可算名詞で扱うことができるのに対して、幾何学的要素は不可算名詞、または物質名詞であると考えることができるでしょう。図形の性質を代数的に扱うときには、図に描けて、一つ二つと数えられて、なにがしかの演算則を持つような、そういった基本の要素を提案する必要があります。

　基本の幾何学的要素としての点は場所を示す概念であって、眼に見えるような寸法を持った材料ではありません。グラフィックスで点を小さな記号で描くのは理解を助けるための手段です。コンピュータのCRTモニターは、例えば800×600個のピクセルで平面領域が埋め尽くされています。幾何で考えている空間は、このような微小な材料で埋め尽くされている「物」ではありません。場所を代数的に数で扱えるようにする手段が座標系です。そして、場所としての点を３次元の座標（世界座標）で表すときに、三つの実数の組(x、y、z)で定義します。

　点の性質に、このような数の概念を持ち込むと、数の演算（＋−×÷）を取り入れた新しい数学量が開発できることになります。幾何学的要素としての点は代数学的な量ではないので、二つの点同士で加減乗除の演算は定義できません。しかし、点を座標の組 (x、y、z)で表すと、ベクトルという代数的な量が定義できて、ベクトルの加減算、ベクトルの積の演算などに約束を決めることができるようになります。今度は逆に、ベクトルを点の表現に使うだけでなく、原点からその点までを繋ぐ向きの定義を持った線分と解釈したりすることもできます。

　基本の幾何学的要素としての直線も、直線状に繋がった場所を表すだけであり、同じく面も平面状に広がった場所を意味するので、それらが小さな点の集合で埋め尽くされているというような、具体的な寸法を持った存在ではありません。直線と面とを座標系の助けをかりて代数的に表したいと考えると、ベクトルとは違った代数学的な量を定義しなければなりません。そして、その定義を踏まえて、平面直線の交点を求める、面と面との交差で直線を求める、といった干渉処理を代数的に計算できるようにします。普通の代数学では、二つ以上の数を一まとめの数学量として記号で表し、記号を使った演算則を定義しているのはベクトルと行列（マトリックス）です。コンピュータ言語のFORTRANでは、データに複素数型を定義できますが、これは平面幾何学の点を代数的な数としてモデル化した唯一の例です。ベクトルと行列の演算を記号式で表すようにした汎用のプログラム言語はありません。

　図形の性質を代数学的な計算で処理させたいとすると、どれだけの種類の数学量（コンピュータ言語の用語ではデータ型と言います）を考えればよいでしょうか、またどれだけの種類の演算則を決めなければならないでしょうか。結論からいうと、型として15種類（表3.1）、演算の約束が13種類（表3.2）ありますので、単純に組合せを計算すると、15×15×13＝2925通りの演算規則を組み立てておかなければなりません。実際には演算が定義できない組合せや、交換則が成り立つ場合もあるので、この数は約200種類に減ります。これでもかなり多い数量です。普通にプログラミングを考えて200種類のサブルーチンを利用するとなると、使い勝手が悪くなります。そのため、データ型という考えを使い、記号式で処理できるようなコンピュータ言語G-BASICを工夫したのです。

　幾何言語G-BASICは、筆者によって1986年に開発され、日本で行なわれた国際会議で発表してあります。この言語の仕様は、8ビットのパーソナルコンピュータPC8000に組み込まれていたBASICインタプリタを真似て、FORTRANで書いたものです。この時代は、まだ32ビットのメインフレームで利用するFORTRANが幅を利かせていましたので、言語の文字仕様は英大文字で書かなければなりませんでした。16ビットの中型コンピュータで動くFORTRANコンパイラを転用して、16ビットのパーソナルコンピュータで利用できるようにしたのがG-BASICの原形です。

G-BASICの解説をすると長くなりますので、ここでは簡単なプログラムを例示します。初等幾何学のごく最初の教育段階で、定規とコンパスとを使い、与えられた三角形の外接円の中心を求める技法を習います。単純な命題ですが、これをG-BASICでプログラミングすると、下に示すリストになります。

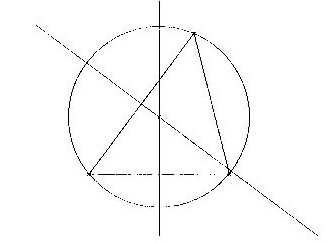
 10 CLS
 20 DEF2PT P
 30 DEF2ED E
 40 DEF2CR C
 50 DEF2LN L
 60 LET PA=-20,-20
 70 LET PB=20,-20
 80 LET PC=10,20
 90 E1=PA@PB
100 E2=PB@PC
110 E3=PC@PA
120 LET LA=LBSEC(PA,PB)
130 LET LB=LBSEC(PC,PA)
140 PR=LA&LB
150 D=DIS(PR,PA)
160 LET C3=PR,D

　上のプログラミングの意味を簡単に説明します。各行の頭にある数字はラベルとしても使う行番号です。変数名は型を宣言して使います。DEFxxxが宣言文で、行番号20、30、40、50で使っていて、それぞれ平面幾何学の点、線分、円、直線の型を指定しています。行番号60、70、80は代入文です。点の型は二つの座標値を持ちますが、内部では配列として扱われます。複数の値を代入するときにLET文でまとめて代入できます。PA、PB、PCは点の型を持った変数名です。行番号90、100、110は、演算子に@を使って三点を結んだ辺を求めます。行番号120、130のLBSECは、二点間の垂直二等分線を求める関数です。これは単純な代入文ですので、LETは省くこともできます。行番号140で外接円の中心PRを二直線の交点として求めます。ここで演算子& を使っています。行番号150で外接円の半径を関数DISを使って計算します。最後に代入文で外接円C3を求めています。このプログラムを実行すると、自動的に作図も行われます。それが図3.1です。