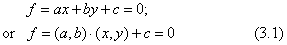
代数学では、1次式y=ax+>bで表される二つの変数x、yの関係を、2次元の(x,y)座標上に直線で描いて示します。このことから、平面幾何学でもこの直線の式を元にして、二つの係数a、bを直線のデータとして利用したいと考えます。しかし、この形は、暗黙の内に三つの幾何学的性質を仮定しています。第一は、y軸に平行に近くなるような急勾配の直線は考えないこと。第二は、直線の正の向きが右向き、つまりx軸の正の向きであること。第三は、直線の上側が正の領域、下側が負の領域であることです。二つの平面直線の交点は、二つの変数xとyとに関する連立方程式を解くことで得られます。しかし、二つの直線式を二組の係数(a,b)で与えて計算させるようなプログラムを組むと、y軸に平行になる直線を与えるときに困ってしまいます。
平面直線が向きの属性を持ち、平面領域を正負の2領域に分けるという考え方は位相幾何学的な属性です。これは直線に向きを決めて、その向きを向いて、左または右、と区別します。向きを決める場合、または左右を区別する場合、これを代数学的には数値の正負で判断します。ちょうど真ん中にある場合に0を当てて、三つの条件を、例えば(-1、0、1)の数値で判断します。このようなことを考えて、任意の勾配と向きを持った直線を平面座標で定義できるようにする代数式を次のようにします。
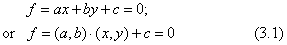
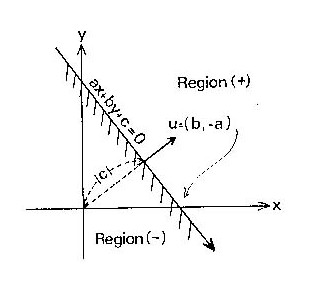
ここで(a,b)、(x,y)は平面ベクトルを表し、記号「・」は二つのベクトルの内積を表すとします。そして三つの数(a,b,c)を一組にしてこれが直線を表すデータであると約束します。上の式に基づく一組の数(a,b,c)>は、全部の定数を一定倍しても代数的には同じ意味です。そこで、図3.2に示した代数直線に下で示すような標準化をして幾何学的な意義を厳密に定義します。
(1) ベクトル(a,b)は直線の方向と垂直であるので、これが単位長さの法線ベクトルになるように(a,b,c)>の数値全部を一定倍する。
(2) 直線に対して法線ベクトルが向く側の領域が正の領域であるとする。向きを逆に定義したい場合には、(a,b,c)の数全部の符号を逆に付け替える。ちなみに、右手系の(x,y)座標系でx軸を表す直線は、法線ベクトルが(0,1)であってy軸の正の向きを表し、(1,0)がx軸の正の向きを定義している。
(3) 上の定義に合うような直線の正の向きは、単位ベクトル(b,-a)の向きになる。この成分を極座標の角度θで表すと(cosθ、sinθ)と表すことができるので、このベクトル成分を方向余弦ということがある。角度θは+x軸から反時計周りに測る角度を正の角度と約束して、全方位を取ることができる。
(4) 平面上の任意の点の座標を位置ベクトル(x,y)で考えると、f=(a,b)・(x,y)+c の計算はその点から直線へ降ろした垂線の、符号付き長さになる。
(5) f=0という条件は、その点が直線上にあることを示し、f>0 とf<0 とは、それぞれ、その点が直線の正側または負側にあることを示す。
(6) c の値は座標原点(0,0)から直線までの距離になり、符号は原点がその直線の正側にあるか負側にあるかを表す。
(7) 原点からこの直線に垂線を下ろした交点の座標は、-c(a,b)で与えることができる。
(8) 直線上の任意の位置を指定するために、上記の交点を基準点として測った長さを変数tとすると、直線の式は下のように表すことができる;
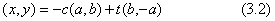
このように標準化した三つの数値の一組(a,b,c)は、平面直線の型を持ったデータであると約束して、内部的には一次元の配列で扱うことにします。
次のページ