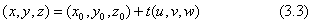
この式を実数直線と言い、座標幾何学の出発となる座標軸の考え方を定義するものです。これを平面上の直線に当てはめると式(3.2)になります。
図形の解析に使うとき、空間直線は無限に延びた細い針金のような実体と考えます。その直線上に基準となる点を位置ベクトル(x0,y0,>z0)で与えます。直線の向きは、単位の方向余弦ベクトル(u,v,w)を決めます。そうすると、直線上の任意の場所の座標(x,y,z)は、一つの実数パラメータtを使って下のように表すことができます;
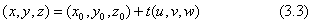
この式を実数直線と言い、座標幾何学の出発となる座標軸の考え方を定義するものです。これを平面上の直線に当てはめると式(3.2)になります。
空間直線を表すとき、直線上の基準点を任意の場所に決めることができますので、標準化した表現を定義するため、この場所は世界座標の原点からの距離が最小になるよう決めるとします。これは、原点からその直線に垂線を下ろした交点になりますので、二つのベクトル(x0,y0,z0)と(u,v,w)とは直交します。この条件は二つのベクトルの内積が0になることです。
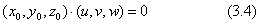
上のように標準化したた六つの数の一組(x0,y0,z0,u,v,w)を、空間直線の型と定義します。直線は向きの定義を含みます。座標系における座標軸の定義も同じ考えの直線です。しかし、座標軸を3本一組で考えることと、3つの基準点が同じ原点であることとを考えると、4つのベクトルを決めればよいことになります。これが2.3節で定義した座標系の定義になります。