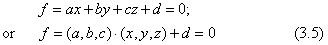
ここに(a,b,c)・(x,y,z)は、二つの3次元ベクトルの内積を表します。そして(a,b,c,d)の四つの数を一組にして、これが面を表すデータであると約束します。幾何学的な意味を含ませるため、データを次のように標準化します:
立体幾何学を扱うときの面は、平面幾何学の直線の性質と似た性質があります。面の性質の表し方で、面がxy座標面に垂直になっている特殊な場合には、面とxy座標面との跡(trace)が2次元の直線の性質になっています。したがって、面を代数的な式で表現する方法は3.2節で説明した方法にならって、標準化したデータ型を定義します。
図3.4 面の定義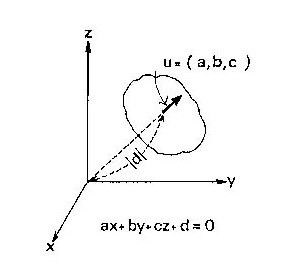
面は空間を二つの領域に分けます。これを区別するため、面に表と裏とを考えます。面の向きを定義するために、単位長さの法線ベクトル n=(a,b,c) を考えます。原点からこの面までの符号付きの距離dを考えて、面を表す代数式を次のように約束します。
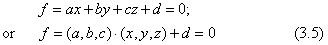
ここに(a,b,c)・(x,y,z)は、二つの3次元ベクトルの内積を表します。そして(a,b,c,d)の四つの数を一組にして、これが面を表すデータであると約束します。幾何学的な意味を含ませるため、データを次のように標準化します:
(1) ベクトル(a,b,c)は、面の向きを表す単位長さの法線ベクトルとする。
(2) 面に対して法線ベクトルの指す側の領域が正の領域であるとする。正の領域を向く側を表、反対側を裏と呼ぶ。多面体の表面は、面の表が見えているとする。
(3) 空間にある任意の点の座標を位置ベクトル(x,y,z)で考えると、f=(a,b,c)・(x,yz)+d の計算はその点から面へ降ろした垂線の符号付き長さになる。
(4) f=0という条件は、その点が面上にあることを示し、f>0 とf<0とは、その点が面に対してそれぞれ正側、負側の空間領域にあることを示す。
(5) dの値は座標原点から面までの距離になり、符号は原点がその面の正側領域にあるか負側の領域にあるかを表す。
(6) 原点から面に垂線を降ろし、面と交わるところの交点の座標は-d(a,b,c)で与えることができる。
このように標準化した四つの数値の一組(a,b,c,d)を、面の型を持ったデータであると約束して、内部的には一次元の配列で扱います。
空間の任意の位置(x,y,z)を考えて、それが与えられた平面に接しているか、離れた位置で表側にあるか裏側にあるかの判定をしたいときには、面を表す一次式に(x,y,z)を代入すれば分かります。逆に、面の上の任意の場所を特定したいときには、二本の直交する空間直線を面上に選んで座標軸とし、面の上に3次元の局所座標系を考えます。二本の空間直線と法線ベクトルとを右手系に選ぶとしても、一つの空間直線の向きの決め方には無限の可能性がありますので、標準化の考え方は保留しておきます。
次のページ