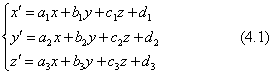
これを行列を使って書くとき、形式的に下のような表現も使います。
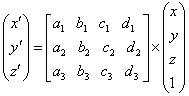
行列(マトリックス)を扱う計算は、連立一次方程式を解くときに代表されるように、もっぱら線形代数の問題に分類されています。しかし、行列の性質を説明するときには、次元、空間、ベクトル、直交などといった幾何学的な用語を使うことが多いものです。特に、現実の2次元、3次元図形を変換する処理では、そこで扱う行列を、幾何学的な性質と結びつけて理解しなければなりません。この章は、主として3次元図形の変換に使われるベクトルと行列の数学を説明します。
立体図形の拡大・縮小・回転・変形・移動などを計算するとき、ある図形の元の座標が、別の座標に変るという関係を一次式の形で考えます。
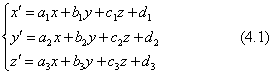
これを行列を使って書くとき、形式的に下のような表現も使います。
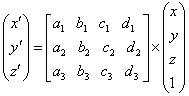
ここで現れる3×4の行列を、変換行列(transformation matrix)と呼ぶならわしになっています。ただし、この表し方は、数値計算に12個のパラメータが必要であるということを、単に行列にまとめたに過ぎません。行列そのものの幾何学的な性質をはっきりさせるためには、下に示すように、3×3の正方行列を使います。
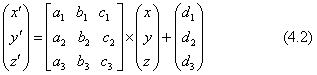
この式を、記号を使って下のような代数式で表します。

ただし、記号は次の約束で用います。

式(4.3) の幾何学的な意味は次のようです。「元の座標pが、行列Tで変換され、さらにベクトルdの方向に平行移動して、座標がqになる」。pを座標軸別の成分に分けて考えますと、
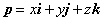
と書けますので、qは下のようにも書くことができます。
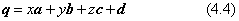
式(4.1) 〜(4.4) は、すべて同じ変換を表しますが、これがどのような幾何学的な意味を持つかを、図4.1を使って説明しましょう。図4.1において、原点を一つの頂点とした単位の正六面体を考えます。その三つの稜線が座標軸を表す単位ベクトルi、j、kで構成されています。この正六面体の各稜線が、ベクトルa、b、cとなった平行六面体に変化し、原点が位置ベクトルdに移動します。式(4.1)〜(4.4) は、このような変換を表したものです。ベクトルa、b、cは、必ずしも単位長さを持つとは限りません。また互いに直交であるとも限りません。その結果、図形が、拡大・縮小・回転・変形の変換をすることになります。この図形の変換は行列Tによって、座標の原点を中心として行なわれ、その後で図形をベクトルdの方向に平行移動させています。
図4.1 変換行列のベクトル成分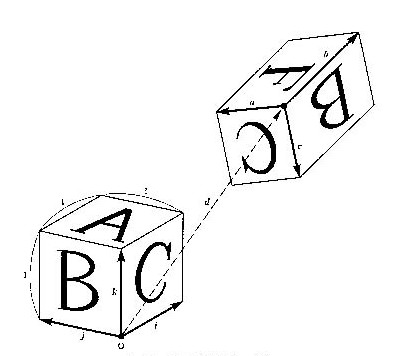
式(4.1) は連立方程式ですから、それを解いた解の意味も理解しておかなければなりません。その問題とは、変換後の座標q=(x',y',z')が分かっていたとして、元の座標p=(x、y、z)を求めることです。このためには、平行移動分dをまず差し引いておいて、行列Tの逆変換、つまり逆行列を演算させます。式で書くと、
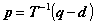
ここで、d’= -T-1dと置けば

変換行列に関して、もう一つ別の考え方があります。それは、世界観を変える変換です。例を挙げて説明しましょう。いま、航空機に乗って外の景色を観察している人がいるとします。その人の見ている景色は、自分の乗っている航空機を基準にして右とか前といったように判断します。これは、航空機そのものに座標系があって、その座標系で位置を計ることを意味しています。空港の方には基準とする座標系(世界座標系)があって、そこから見た航空機の位置と向きは、動く座標系(局所座標系) であると考えます。局所座標系の座標軸の向きと原点の位置は、世界座標系で測った三つの座標軸方向を示す単位ベクトルa,b,cと、位置ベクトルdとで与えます。航空機に乗って見た世界は、座標p=(x,y,z)で測りますが、これを世界座標系に直せば、q =(x'、y'、z')になります。その関係を表す変換式が式(4.3)です。四つのベクトル(a,b,c,d)をまとめた最初の3×4の矩形行列は、座標系を定義するデータとしても使います。
同じような世界観の変換は、テレビを見ている人と、ビデオカメラとの関係にあてはめて考えることができます。テレビを見ている人は、自分の眼の前にある映像が、あたかも眼の前の現実のように観察しますが、それはビデオカメラの座標系で観察した世界です。ビデオカメラには、レンズの光軸を一つの座標軸とするような座標系を考えることができて、世界座標の中で、座標軸の向きを示す三つのベクトルa,b,cとビデオカメラの位置をベクトルdで考えることにします。つまり、ビデオカメラ本体は、同じく3×4の矩形行列(a,b,c,d)で決まる局所座標で定義します。さて、テレビを見ている人が、あたかも現実の場所と見間違えている二次元の景色は、奥行きを補いながら観察しますが、ビデオカメラの世界で見た座標p =(x,y,z)であって、それは景色が実際にある場所の座標q =(x',y',z')を写したものです。コンピュータグラフィックスの課題は、qが与えられて、映像のデータp =(x,y,z)を求めることですので、数学的な課題は、逆変換を表す式(4.5) の方になります。映画のワイドスクリーン用のカメラでは、縦横の比率を変えて撮影します。これは、座標軸を定めるベクトルa,b,cの長さがすべては等しくなく、世界をいびつに眺めています。これを式(4.5) の逆変換の関係式でいうと、元の座標系の原点がd'にあるように見え、最初の座標軸のベクトルi,j,kが長さも方向も変わって、逆行列T-1=(a',b',c')の成分のように見えるのです。
変換行列は、ロボットの動作を幾何学的にシミュレートさせるときにも重要なデータです。ロボットの部品と部品のつながりは、親から子、子から孫、孫から曾孫、…の階層構造でつながっています。部品それぞれには、固有の座標系が付与されているものとします。部品の親と子の位置関係は、親の座標系から見て、子の座標系がどう見えるかを定めることです。ロボットの動作は、親と子、子と孫、孫と曾孫、…のような直の間柄の相対的な動きが積み重なったものです。親に対する子の動きは、変換行列で定義します。親に対して子が相対的に動けば、子に付随している孫の座標系も動きます。そして、子にぶらさがっている孫、曾孫、…も、つられて動きます。ロボットのシミュレーションを行うとき、3×4の変換行列を2種類に使い分けます。一つは座標系を定義するデータとしてであり、もう一つは、相対運動を定義するデータです。座標系そのものも相対運動の対象です。図4.2は、ロボットのシミュレーションの例であって、プログラムパッケージGEOMAPで作図したものです。
図4.2 ロボットのシミュレーション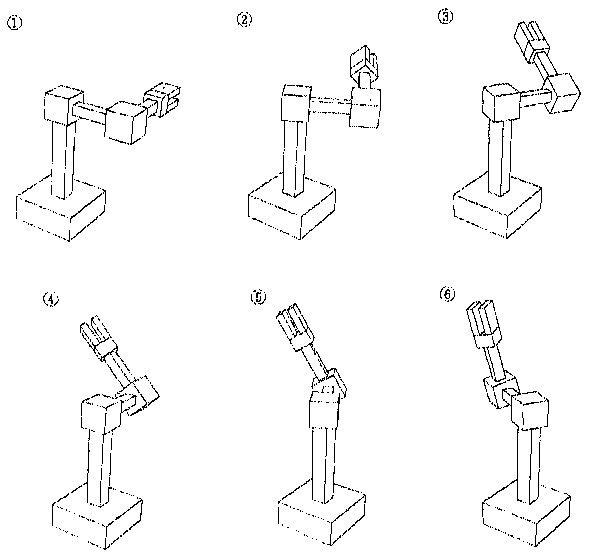
10 PRINT "GEOMAP Demonstration Program"
20 PRINT "--- Moving and Deformation of Models ---"
30 DIM BSIZE(3,9),AXIS(3,2),NAME$(9)
40 READ BSIZE : REM ------ DATA FOR BSIZE ------
50 DATA 20 15 5, 20 15 5, 10 15 15, 30 8 8, 3*20
60 DATA 8 30 8, 3*20, 12 12 65, 50 50 20
70 READ AXIS : REM ------ DATA FOR AXIS ------
80 DATA 5 5 0, 1 0 0
90 READ NAME$ : REM ------ NAMING FOR BODIES ------
100 DATA "A1","A2","A3","A4","A5","A6","A7","A8","A9"
110 REM ============================== DPCAM
120 CAM(1)=300: CAM(2)=200 : CAM(3)=180 : TH=0.8
130 DPCAM CAM,TH
140 CMINIT : REM ===================== PCUBE
150 FOR I=1 TO 9
160 PCUBE NAME$(I), BSIZE(1,I), BSIZE(2,I), BSIZE(3,I)
170 NEXT I
180 REM ============================== LMTREE
190 FOR I=3 TO 8
200 LMTREE NAME$(I+1),NAME$(I)
210 NEXT I
220 LMTREE "A3", "A1", "A2"
230 REM ============================== PGDIS
240 DIS(1)=-15: DIS(3)=5 : PGDIS "A1",,DIS
250 DIS(3)=-5 : PGDIS "A2",,DIS
260 DIS(1)=-20 : DIS(3)=0 : PGDIS "A3",,DIS,1
270 DIS(1)=-25 : PGDIS "A4",,DIS,1
280 DIS(1)=0 : DIS(2)=25 : PGDIS "A5",,DIS,1
290 DIS(1)=0 : PGDIS "A6",,DIS,1
300 DIS(2)=0 : DIS(3)=42.5 : PGDIS "A7",,DIS,1
310 DIS(2)=0 : PGDIS "A8",,DIS,1
320 DIS(3)=-50 : PGDIS "A9",,DIS,1
330 REM ============================== PGROT
340 ANG1(1)=30 : ANG2(2)=15: ANG3(3)=45 : ITREE=1
350 CLS : HFDISP "A9",1,0
360 FOR I=1 TO 5
370 PGROT "A3","A3",ANG3,CEN(1),ITREE
380 PGROT "A5","A5",ANG2,CEN ,ITREE
390 PGROT "A7","A7",ANG1,CEN ,ITREE
400 CLS : HFDISP "A9",ITREE
410 NEXT I
420 REM ============================== PGFACT
430 PGFACT "A9",,CEN,-0.5,ITREE
440 CLS : HFDISP "A9",ITREE
450 PGFACT "A9",,CEN,-1.0,ITREE
460 CLS : HFDISP "A9",ITREE
470 REM ============================== PGPAN
480 PGPAN "A9",,AXIS,2.0,ITREE
490 CLS : HFDISP "A9",ITREE
500 REM ============================== PGLONG
510 PGLONG "A9",,AXIS,-2.0,ITREE
520 CLS : HFDISP "A9",ITREE
530 END