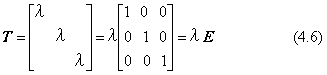
ただし、上の対角行列で、λは倍率を表し、|λ|>1であれば拡大、|λ|<1は縮小です。立体図形の、体積拡大または縮小率κは、寸法比がλ倍であるので、

λは 普通正の値です。もし負の数、λ<0である場合は、変換によって各座標軸方向に長さが|λ|倍になると同時に、対応する座標位置が原点に対して反対側に移動します。また、結果として左右が反転するような鏡像変換を伴います。
立体図形を単純に拡大または縮小させるときの、変換行列Tの一般的な形は、
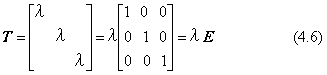
ただし、上の対角行列で、λは倍率を表し、|λ|>1であれば拡大、|λ|<1は縮小です。立体図形の、体積拡大または縮小率κは、寸法比がλ倍であるので、

λは 普通正の値です。もし負の数、λ<0である場合は、変換によって各座標軸方向に長さが|λ|倍になると同時に、対応する座標位置が原点に対して反対側に移動します。また、結果として左右が反転するような鏡像変換を伴います。
例として、まずx軸方向にλ倍に拡大または縮小するときの変換行列を示します。
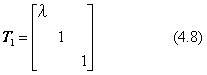
ここで、|λ|>1であれば拡大、|λ|<1は縮小です。λの符号が負であると、(y,z)座標面を鏡面とするようにx座標軸の対応位置が左右反転します。この場合の図形の変換は、相似な図形変換ではなく、変形を伴います。同様にy軸、またはz軸方向にλ倍するときの変換行列は、それぞれ下のようになります。
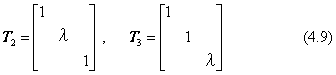
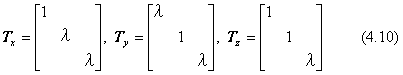
座標軸方向に、拡大・縮小を個別に実行させる式は(4.8)、(4.9)です。この変換を一度に実行させる変換行列は、次の対角行列です。ただし、λ1、λ2、λ3は、各座標軸方向ごとの拡大または縮小の倍率です。
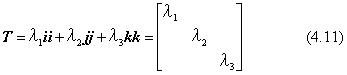
立体図形の拡大・縮小を考えるとき、任意の方向に引き伸ばしたり圧縮させたりする変形を考えておく必要があります。方向の指定は、単位ベクトルu=(u1,u2,u3)で与えます。後の説明で必要になるので、ついでに定義しておきますが、ベクトルuの他にもう二つの単位ベクトルvとwが必要になって(u,v,w)が互いに直交し、かつ右手系の位置関係になるように決めます。拡大・縮小を考えるには、中心を決め、そこを起点とした膨張または収縮をさせます。この中心については、4.2.8
項で説明しますが、ここでは、その中心が原点にあるとしておきます。ベクトルuの方向の倍率をλ、それと直交する2方向には倍率が1です。変換行列は次のようになります。
T=λuu+vv+ww
ここで、単位行列が、E=uu+vv+ww となることを代入すると、vとwの項を含まない式が得られます。

一つの軸を中心として、同心円状に立体図形を拡大または縮小させることを考えます。軸の向きは、単位ベクトルuで与え、中心軸は、差当って原点を通るとしておきます。軸の位置ぎめの説明は、4.2.8 項で説明します。変換行列は次のようになります。
T=uu+λ(vv+ww)=(1-λ)uu+λE
行列の成分で示すと、下のように得られます。
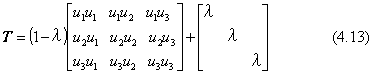
互いに直交する三つの単位ベクトル(u,v,w
)の方向に、それぞれの倍率がλ1、λ2、λ3であるような拡大・縮小は、次の変換行列で与えます。

立体図形の体積の拡大または縮小の倍率κは、3方向の倍率の積κ=λ1λ2λ3で与えられ、Tの行列式|T|に等しくなります。κには符号があり、これが負の値になるときは、立体図形は、鏡に写った像のように左右が反転する変換を伴います。式(4.14)は固有値解析をするときに現れますが、この説明は4.7節で扱います。
いままでの説明は、すべて、原点を中心として図形を拡大または縮小させる場合について、行列Tがどのように表されるかを示しました。拡大・縮小を考えるときには、爆弾でいえば爆発の中心に相当する場所を指定する必要があります。この位置をp0=(x0,y0,z0)とします。4.2.3項、および4.2.6 項で説明したような、ある軸を中心として2次元的に拡大・縮小を考えるとき、その軸の上に1点を決め、その座標をp0とします。
変換の操作は、次のように考えます。まず、立体図形全体を−p0のベクトル方向に平行移動させ、拡大・縮小の中心点を原点に移します。行列Tによって原点を中心とした拡大・縮小の処理を施します。その後で、再びベクトルp0の方向に図形を平行移動させます。この操作を式に書くと、
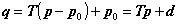
すなわち
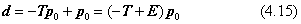
のようにdを決めることができます。