4.3 変形を伴わない回転

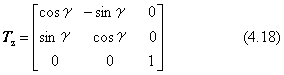
　立体図形を、変形させないで回転させる変換は、力学では剛体の運動を扱う計算の中で用いられます。この変換は、ロボット工学などと関連して、コンピュータグラフィックスやソリッドモデリングでの基本的な処理として用途が広いものです。図形を回転させる変換行列を計算するには、回転軸と回転角度を決めなければなりませんが、まずその前に、思考実験で頭の中で図形の回転が想像できなければなりません。いちばん分かり易い方法は、大きなサイコロ状のモデルを手に持って、自分の眼の前に座標系を仮定し、モデルの回転を試して納得することが大切です。この節の説明の大部分は、回転軸が原点を通る場合について述べてあります。回転軸が原点を通らない場合の一般式の求め方は、後の4.3.7項で解説します。変換行列を別の座標系で定義する方法などは、4.4節で説明します。

4.3.1 回転を与える行列の一般的な性質

　ある図形の元の座標pが、原点を通る回転軸によって回転し、その座標がqに変わる関係式は、行列を使った次の式です。

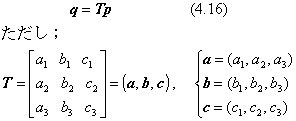
行列Tは、座標軸の単位ベクトルを用いた二項積で表現できます。

この行列は、座標軸を表すベクトル(i,j,k)を、それぞれベクトル(a,b,c)に変換することを意味しています。(i,j,k)が右手系の互いに直交する単位ベクトルですので、これらの変換後のベクトル(a,b,c)も、右手系の互いに直交する単位ベクトルでなければなりません。この性質を満たすことが、変形を伴わない回転をさせる変換行列の条件です。

4.3.2 z座標軸回りの回転

通常のデカルト座標系の約束では、垂直で上向きをz座標軸とし、その方向はベクトルkで与えます。このベクトルの正の向きを向いて、右回りの回転角をγで表すことにします。回転によって、モデルに付いている座標軸のベクトル(i,j,k)が次のように位置を変えて、ベクトル(a,b,c)になります。なお、この回転は、２次元平面図形を(x,y)座標の上で回転をさせるときの回転の定義でもあります。平面図形は左回りに回転させるのを正の向きの回転と決めますが、これは３次元空間を上から下に向いて見ていることになっています。

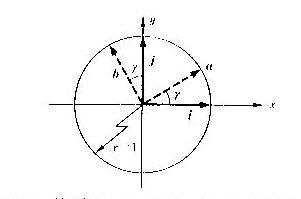
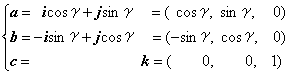
これによって、z軸回りの回転を与える行列は、a,b,cを縦ベクトルとして、

4.3.3 y座標軸回りの回転

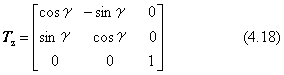
　y座標軸の方向はベクトルjの方向で与えます。このベクトル方向に右回りの回転角をβで表します。回転によって、ベクトル(i,j,k)が次のように位置を変えて、ベクトル(a,b,c)になります。

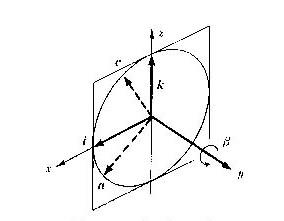
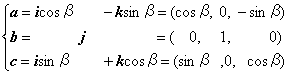
y軸回りの回転を与える行列は、a,b,cを縦ベクトルとして並べます。

4.3.4 x座標軸回りの回転

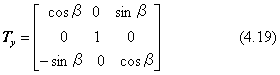
　x座標軸の方向はベクトルiです。このベクトル方向に右回りの回転角をαで表します。回転によって、ベクトル(i,j,k)が次のように位置を変えて、ベクトル(a,b,c)になります。

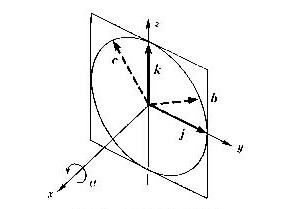
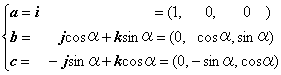
x軸回りの回転を与える行列は、a,b,cを縦ベクトルとして並べたものです。

4.3.5 回転の合成

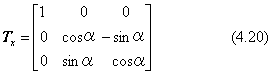
　立体図形を任意の向きに回転させたいとき、上で求めた式(4.18)〜(4.20)の座標軸回りの回転を３回続けます。回転に使う座標軸の順序は任意に選ぶこともできますが、普通は世界座標のx軸、y軸、z軸の順序とし、これをオイラー回転と言います。計算の結果を示すと、変換行列が次のようになります。

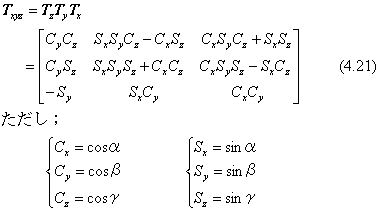
　立体図形を回転させると、この図形に付属している局所座標系も一緒に回転します。したがって、局所座標軸の向きが変わってしまいます。ここでの式は、回転軸を世界座標系の座標軸で考えていますので、立体図形の座標軸の動きを考える必要がありません。回転軸を回転させる図形の方の座標軸で考えるときの回転行列の求め方は、4.4節で説明します。

4.3.6 任意の方向を向いた回転軸による回転

　ロボットの運動を定義したいときのように、あらかじめ回転軸が決まっていて、それを軸にした回転運動を求めたいことがあります。ここでの説明は、その軸が座標軸の原点を通る場合の式です。まず、回転軸は、単位ベクトルu=(u₁,u₂,u₃)の方向で与えることにします。回転角はベクトルuの方向に右回りの回転角をθで表すことにします。式の誘導には、ベクトルuの他にもう二つの単位ベクトルvとwが必要であり、(u,v,w)が互いに直交し、かつ右手系の位置関係になるように決めておくとします。

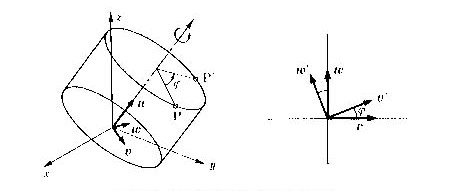
立体図形の座標pをu、v、wの成分で表すと、下のような二項積です。

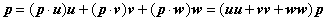
変換はpがqになることです。

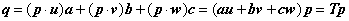
ここで、もとの座標軸(u,v,w)が、新しい座標軸の向き(a,b,c)に変換されます。その向きは、

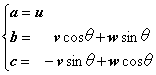
変換行列つまり回転行列Tを、すべてu、v、wで表すようにしますと、

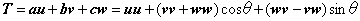
ここで、(uu+vv+ww)は単位行列Eになります。また、(wv-vw)を行列の成分で表すと、結果的にベクトルuの成分だけで表すことができます。これらを代入すると、行列Tを次のように表すことができます。

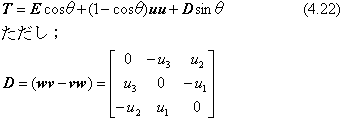
　式(4.22) において、ベクトルuに座標軸のベクトル(i,j,k)の成分をそれぞれ当てはめると、4.3.2項から4.3.4項までに説明した式(4.20)、(4.19)、(4.18) になることを確かめることができます。

4.3.7 回転軸が原点を通らない場合の回転

　いままでの説明は、すべて、原点を通る軸を回転軸として、図形を変形させないで回転させるときの行列Tを、いくつかの場合で示しました。つまり、変換の標準形であるq=Tp+d (式(4.3))で、d=0の場合を説明しました。本項では、dの値を決める方法を示します。回転軸を表す空間直線の定義方法にはいくつかあります。ここでは、直線上の一点p₀と直線の方向を決める単位ベクトルuとで考えることにします。この決め方は、3.3節で解説した空間直線の定義方法に従っています。

　変換の操作は、次のように考えます。まず、立体図形全体を-p₀のベクトル方向に平行移動させ、回転軸が原点を通るようにします。行列Tによって原点を通る回転軸で回転処理を施した後で、再びベクトルp₀の方向に図形を平行移動させます。この操作は、4.2.8項の説明と全く同じです。したがって、式も同じですが、念のためもう一度示します。

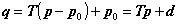
ここで、dは

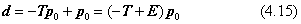
のようにdを決めることができます。