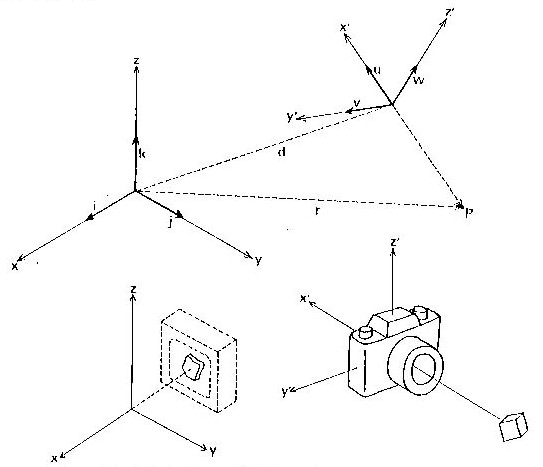
いくつかの部品がヒンジなどで連結されているロボットの機構では(図4.2参照)、各部品ごとに独立した局所座標系(LC)を持たせ、この座標系でその部品の各所の位置を表したり、変換を指示したりするのが便利です。この座標系は、部品に固定され、部品が動けば部品とともに回転したり移動したりします。座標系と図形の変換は、いずれも式の形は同じように4.1節で説明した3×4の行列です。世界座標系を記号WC、局所座標系を記号LC、変換行列を記号TMで表すとして、まず、この節で説明する問題の分類を示します。
(1)2回に分けて処理される変換TM-A、TM-Bを1回の処理に合成する。
(2) 座標系LC-Aが、変換行列TM-Bで移動と回転をする。
(3) 座標系LC-Aが座標系LC-Bの中で間接的に定義されているので、世界座標系WCで定義し直す。
(4) 座標系LC-Aで定義されている変換TM-Bを、世界座標系WCで見た変換に直す。
(5) 世界座標系で定義された変換TM-Bを、座標系LC-Aで定義すること「(4) の逆問題」。
最後の二つ(4)と(5) は、座標系の変換に関するものです。この節では一般的な式を挙げるだけにしますが、二項積での表現は4.4.6項で扱います。
図形の変形・回転・移動を処理させる二つの変換行列をA、Bの指標をつけて、次のように表すことにします。
・図形の変換を表す行列-A: (aA, bA, cA,dA)=(TA, dA)図形上のある一点の座標p は、まず変換行列Aで変換されてp' になり、ついで変換行列Bで変換されてq になるとしますと、
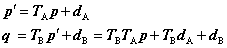
すなわち、2回の変換処理を1回の変換処理として表す変換行列を(TC, dC)で表すと、次の表現が得られます。
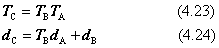
もし変換の順序が違うとき、たとえば、最初に変換B、次いで変換Aの順序で変換をさせると、上と違った結果が得られます。座標軸回りの回転だけで立体のモデルを任意の向きに向かせたいとき、三つの座標軸を選ぶ順序を決めて3回の変換をさせます。座標軸の順番の選び方は何通りもあります。4.3.5項の式(4.21)は座標軸回りの回転を行わせる順序のうち、よく使う一つを示したものに過ぎません。付録Bは、この座標軸回りの回転の組合せのすべての場合を表にまとめたものです。また、付録Cは立方体の置き方が24通りあって、その場合の回転行列をまとめたものです。
ある部品Aの座標系は、座標軸の方向を表す3つのベクトルと、原点の位置を示す位置ベクトルで表します。座標系の運動も、3×4の変換行列Bで表しますが、この成分も、剛体回転を表す3×3行列と平行移動のベクトル成分で与えます。
・部品Aの座標系を表す行:(aA,bA,
cA,dA)
=(TA,dA)
・移動、回転を表す変換行列:(aB,bB,
cB,dB)
=(TB,dB)
移動、回転の変換処理を受けた後の座標系を表す行列を(TA', d A')で表せば、これは次式で計算されます(図 4.1)。
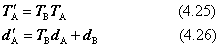
ここで、式(4.23)、(4.24)と (4.25)、(4.26)は、それぞれの右辺が全く同じ表現であることを確かめて欲しいのです。ただし、4.4.1項の図形の変換の場合は、図形に変形を起こさせる変換であっても差し支えありません。しかし4.4.2 項の場合の行列TA、TBの場合、いずれも4.3節で解説した剛体回転の変換をさせる行列の性質を満たさなければならないのです。
図 4.7 座標系の移動と回転(立方体の辺で表した)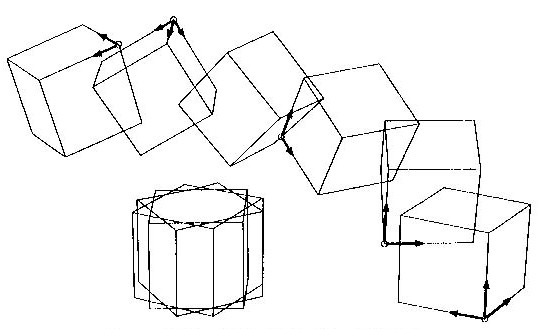
ロボットの二つの部品A、Bの接続を考えます。部品Bが親で、部品Aが子の関係とします。部品Aの、部品Bに対する位置関係を表したいとき、部品Bから見た部品Aの座標系を与えるのが便利です。そこで、座標系Aは、世界座標系で見ればどうなるでしょうか? 座標系も3×4の行列で表すので、記号を次のように約束しておきます。
・部品Aの座標系(座標系Bで定義):(aA,
bA,cA,
dA)=(TA,
dA)
・部品Bの座標系(世界座標で定義):(aB,
bB, cB, dB)=(TB,
dB)
座標系Aを世界座標で見たときの行列を(TA', d A')の記号で表します。この値を与える式は、前項の式(4.25)、(4.26) と全く同形です。すなわち、以上の三つの処理では式の形がすべて同じであるので、問題の基本である幾何学的な意味を十分に認識して応用しなければならないのです。
いくつかの部品がヒンジなどで連結されているロボットの機構では、部品Aにつながっている別の部品Bの運動を表す必要が生じます。これを変換行列をBとします。変換行列Bは、部品Aの座標系を基準にして表すのが便利です。しかし、この変換Bを世界座標系でどのように動くかを求めておかなければ、現実の運動を表すことができません。そこで、記号を次のように約束します。
・部品Aの座標系(世界座標で定義):(aA,
bA, cA,dA)=(TA,
dA)
・部品Bの運動を座標系Aで定義する:(aB,
bB, cB, dB)=(TB,
dB)
・部品Bの運動を世界座標で定義する:(a, b,
c, d )=(T, d )
部品Bの、ある一点を世界座標で計った位置をpとします。この点を座標系Aで見たときの座標をp'とします。pとp'との関係は、4.1節で説明した式(4.3)、(4.5)を当てはめます。
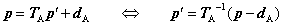
ただし、TA-1は、行列TAの逆行列です。なお、逆行列の求め方は後の節で説明しますが、TAが座標系を表す場合には、この転置行列が逆行列と等しくなります。p'は、部品Bの運動を与える変換行列によってその位置がq'に変換されます。
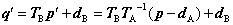
q'は座標系Aで表した変換後の位置です。したがって、q'を世界座標で見たときの座標をqとすると、
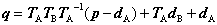
すなわち、この変換を式(4.3) の標準の変換の式q=Tp+d の形で表すようにしますと、Tとdが次の式で与えられます。
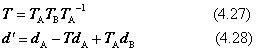
この項の説明は、上の4.4.4項の逆変換です。いま、世界座標系で、部品Bにある運動をさせたいとします。この動きを部品Aから眺め、部品Aの座標系で定義すると部品Bの部品Aに対する相対的な変換になります。この変換を求めたい、というのがここでの解説です。これは部品Aの座標系で見た部品Bの変換です。記号を次のように決めておきます。
・部品Aの座標系(世界座標で定義):(aA,
bA, cA,dA)=(TA,
dA)
・部品Bの運動を座標系Aで定義する:(aB,
bB, cB, dB)=(TB,
dB)
・部品Bの運動を世界座標で定義する:(a, b,
c, d )=(T, d )
世界座標で定義されたある一点の座標をp、その変換後の座標は、q=Tp+dです。 pとqを、座標系Aで表したものを、p'、q'とすれば、q= TAq'+ dA およびp= TAp'+ dA の関係があるので、これらの関係を代入すると、

結果として下の表現が得られます。これは式(4.27)、(4.28)の逆変換です。
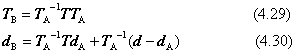
人工衛星の姿勢制御を想像してみましょう。衛星の位置は、地球の中心を仮に原点と仮定した宇宙座標系で考えます。理由は、地球自身も自転しているからです。衛星自体は、その自分自身の座標系Aを基準として自分の姿勢を変えます。この変換は、座標系Aに基づいての変換行列Bで与えます。この変換を宇宙座標系で眺めていると、座標系Aが変換されて見えます。変換後の座標系A'を求めようというのがここでの問題です。これは今まで説明した2種類の変換を組み合わせたものです。まず、4.4.4項で述べた「局所座標系Aで定義した変換行列Bを世界座標系で定義しなおす」こと。ついで4.4.2 項で述べた「座標系Aを変換する」操作を行わせ、新しい座標系A'を求めます。記号を次のように約束します。
・部品Aの座標系(世界座標で定義): (aA,
bA, cA, dA)=(TA,
dA)
・部品Aの運動を座標系Aで定義: (aB,
bB, cB, dB)=(TB,
dB)
・部品Aの変換後の座標系(世界座標): (aC,
bC, cC, dC)=(TC,
dC)
変換行列(TB, dB)を世界座標での定義に直した変換行列(T,d)は、式(4.27)、(4.28) に示しました。新しい座標系は、式(4.25)、(4.26) を利用して求めます。

4.4.6項までの説明は、いわば公式の誘導です。この応用として、ここでカメラの位置決めに使われている変換を解説しましょう。我々が身近に使うカメラは、3次元空間での移動・回転をさせる物体としての性質を持つと同時に、我々の眼を代表してカメラの眼で世界を見る役目を果たします。これはカメラの座標系で世界を見るので、座標変換をしていることになるからです。
カメラを3脚の上に乗せ、カメラを動かして被写体をファインダの中央にとらえる操作を想像して下さい。このとき、カメラを上下左右には動かさないものとします。まず、カメラを水平にしたまま左右に回転させます。これを、カメラの専門用語ではパン(pan) と言います。次に、人がお辞儀をするように上下に振る。これをスイング(swing) と言います。この連続した二度の回転で、大抵の被写体をカメラのファインダにとらえることができます。それから、カメラを手に持って被写体を狙うとき、被写体をレンズの中心でとらえたまま、頭を左右に傾けて像の写る角度を変えます。これをティルト(tilt)と言います。
カメラの回転を制御するパン・スイング・ティルトを幾何学的に定義するためには、カメラ本体に座標系を決めておく必要があります。この約束は、図4.8 に示すような右手系の座標系を仮定します。カメラを手に持って構えた状態で、z軸は垂直で上向き、y軸は右腕を水平に上げた方向、x軸はファインダを見る方向とは逆に、後向きを正の方向と約束します。まず、パンは、z軸回りのカメラの回転γであって、左に向きを変える方向が正の回転方向になります。スイングは、上を向く方向に回転させる角度βを正の向きとします。ティルトは、頭を左に傾ける角度αを正の向きとします。これらの正負の向きの約束は、座標軸の正の向きに向いて右回りに回る方向を正の回転と定義することです。
回転軸に使う座標軸を除いた他の座標軸はカメラと一緒に回転しますので、どの座標軸を次の回転軸にするかの順番が変われば、全く違った方向にカメラが向くことになります。したがって、実用的には、回転の順番をパン・スイング・ティルトの順に決める約束にします。最初、カメラの座標は(TA, dA)です。変換は、カメラ座標系の原点を通る座標軸で回転させると約束します。パン・スイング・ティルトの変換行列は、 4.3.2〜4.3.4 項の式 (4.18)〜(4.20) ですでに与えてある行列Tz、Ty、Txを使います。式(4.31) を応用すると、座標軸回りの回転を3回させることにより、座標系Aは、次のように変化します。
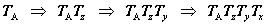
ここで、4.3.5項で求めたオイラー回転を与える行列、式(4.21)を参照してほしいのです。すると、カメラの変換は次のようになっていることがわかります。

もしカメラの回転を、世界座標の座標軸で回転させる場合には、行列の積の順序が逆になっていることに注意します。つまり

ここで、カメラの最初の座標軸の向きが世界座標系>Eと平行であれば、式(4.33) と (4.34) とが同じ結果になります。
図 4.8 カメラに付属させるカメラ座標系