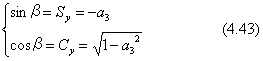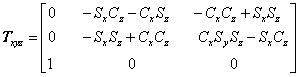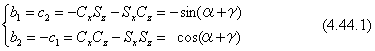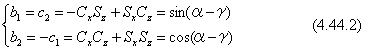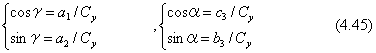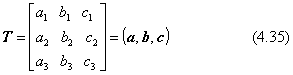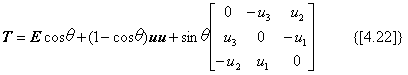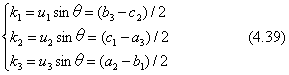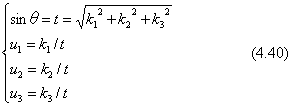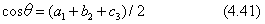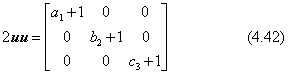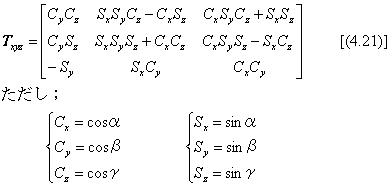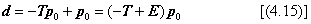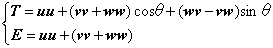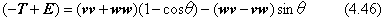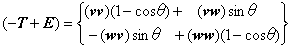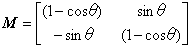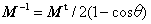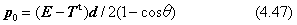4.5 回転を与える変換行列の解析
前のページ;
次のページ
第4.3節では、立体図形を変形させないで、力学でいう剛体の回転を扱う3×3行列の求め方を説明しました。この節は、4.3節の逆問題を扱います。つまり、3×3行列が与えられたとして、この回転軸の方向、回転角度および回転軸が通る位置を求めることです。この計算において扱うことができる行列は、行列の要素について、いくつかの条件を満足していなければなりません。最初にこの条件を吟味し、ついで、回転軸と回転角度を求める式を説明します。
4.5.1 回転を与える変換行列の条件
図形の変換を表す一般的な関係式は、すでに式(4.3) で説明したようにq=Tp+dの形です。回転を行わせる3×3の行列Tの要素を、下のように三つの縦ベクトルの要素で表すことにします。
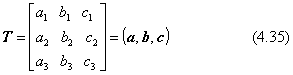
行列Tが剛体回転をさせる変換行列である条件は、ベクトル(a,b,c)が、右手系の互いに直交する単位ベクトルでなければならないことです。式で示すと次の条件です。

行列Tは、式(4.35) に示したように9個の要素があります。しかし、要素同士は式
(4.36)〜(4.38) の条件を満たさなければなりませんから、要素の値を決定する自由度は3個しか残りません。上の条件が満たされますと、Tの逆行列T-1は転置行列Ttに等しくなります。また、逆行列は、幾何学的にいえば、回転を元に戻す変換ですので、元の行列の転置行列についても、式(4.36)〜
(4.38)と同じ条件が成り立ちます。この条件を満たした3×3行列を回転行列と呼ぶことにします。
4.5.2 回転軸の方向と回転角を求めること
3×3の行列Tが回転行列であるとき、一つの軸を決めて、ただ一回の回転操作で所望の回転を実現させることができます。そのときの回転軸の方向を単位ベクトルu=(u1,u2,u3)、回転角をそのベクトル方向に右回りにθとすると、行列Tは、式(4.22)
で表すことができます。説明のため、その式を再掲します。
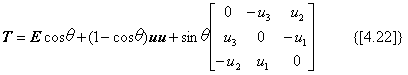
式(4.22) の行列は、パラメータとして(u1,u2,u3,θ)の4個が使われていますが、uが単位ベクトルである条件が1個必要です。式(4.22)の右辺の逆対称の成分が、回転を与える行列の特徴ですので、この要素に注目すれば、ベクトルuの成分を求めることができます。すなわち、
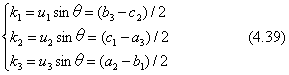
ベクトルuが単位ベクトルですので、u・u=1 の条件を満たすようにすることで、sinθの値を求めることができます。
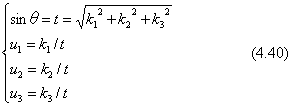
なお、式(4.39) において、ベクトルuの向きを逆に定義すると、θの符号も反転します。cosθの値を求めるには、まず、式(4.35) と式(4.22)の行列から、対角線要素だけに注目します。
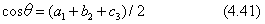
sinθとcosθとが求まれば、θを確定できます。
もし行列Tの非対称成分がすべて0であれば、θが0度または180度のどちらかであり、行列Tの対角線要素が1または-1のどちらかになります。このときは、全く回転をしないか、座標軸回りに180度の回転をするときに当たります。このときは、式
(4.39) 、(4.40)、 ではなく行列Tの対称成分を使った下の式を参考にして求めます。
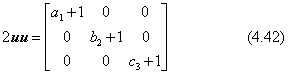
付録Cには、サイコロ状の立方体の向きが24通り示されていますが、これは座標軸回りの回転が90度の倍数の場合の回転行列をすべて示したものです。向きの分類コードでB3、E3、E1が式(4.42)の条件に当たります。
4.5.3 座標軸回りの回転角度を求めること
任意の向きに幾何モデルを回転させるとき、世界座標系のx軸、y軸、z軸の順に回転させるのが標準の考え方になっています。この計算式は、4.3.5節の式(4.21)に示してありますが、説明のため、この式をもう一度下に示します。ここでの問題は、式(4.35)に示した行列の要素から、座標軸ごとの回転角度α、β、γを求めることです。理屈の上では座標軸の順番の決め方が6通りあります。しかし、座標軸の選び方はかなり恣意的ですので、回転させる軸の順序に仮のx、y、z軸を当てはめて考えることができます。回転角度の正の向きの定義が座標軸の向きと合わなければ、角度の正負の定義を反対にすればよいので、式(4.21)に基づいた解析方法は他の場合にも応用できます。
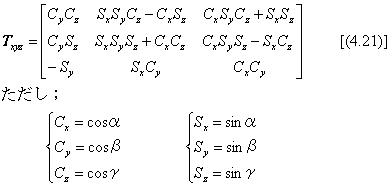
回転角度α、β、γを求めるには、代数的に未知数と条件式とを対応させながら、ある程度の論理的な判断をする必要があります。
(1) まず、式(4.35) と式(4.22)を比較すれば、角度βについて
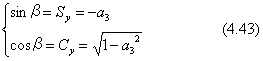
パラメータCyは、負の符号の可能性がありますが、差当ってCy>0と決めます。これは、角度βの範囲を±90度(-π/2、π/2)の範囲と指定することです。
(2) もしも|a3|=1 であれば、a1、a2、b3、c3がすべて0です。このときには、次の二つの場合があります。
(2a) a3=1のとき、β=-π/2です。式(4.21)は、下のように簡略化されます。
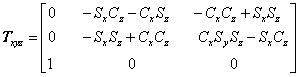
すなわち、与えられた行列の要素に、次の関係が必要です。
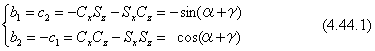
(2b) a3=-1のとき、β=π/2です。式(4.21)は、下のようになります。
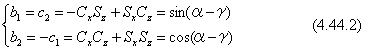
二つのケースを比較すると、α=0とおくことでβの符号を気にしないで済みます。つまり下の式(4.45)で、角度γを求めることができます。
(3) |a3|<1 であるとき、βは式(4.43)で求められます。角度αとγについて、次のように決まります。
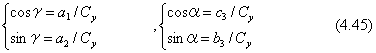
4.5.4 回転の中心を求めること
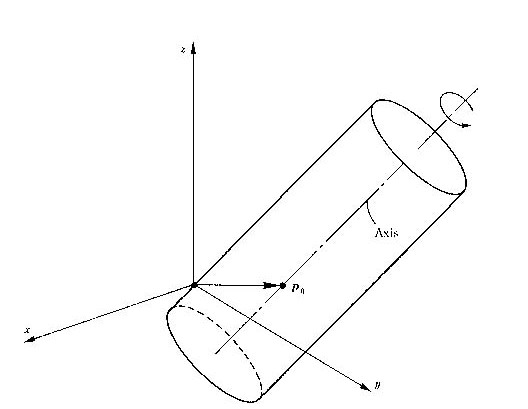
立体図形を回転させる変換q=Tp+dにおいて、回転軸が原点を通らない場合に平行移動のベクトル成分dを決めておくことが必要です。このdの求め方は、4.2.8項で説明しました。回転軸が位置ベクトルp0 を通るとき、dとp0の関係を、式(4.15)で与えてあります。再掲すると下式です。
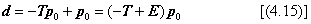
この項で説明しようとしているのは、Tとdから、p0を求めようという逆問題です。
図 4.9 回転軸が通る位置
いま、d=(E-T)p0と書くことができますから、(-T+E)の逆行列が求められればdを与えてp0を計算することができます。しかし、EとTは、4.3.6項の説明では、下に示すような二項積で表すことができました。
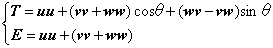
したがって、
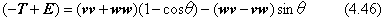
ここで、(-T+E)は、ベクトルuの成分を全く含まないので、正則の行列になっていません。つまり、(-T+E)の逆行列を求めることができないのです。実は、このことは当然予想されることなのです。その理由は、p0が回転軸上にあれば、その軸上のどこにあってもよいからです。p0が一つの解であれば、λを任意に選んだスカラーとしてp0+λuもまた解になるからです。式(4.46)を、vとwとの二項積の成分で行列に並べ直した一次形式で示しましょう。
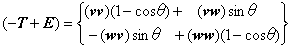
係数だけを取り出した2次元の行列をMとします。
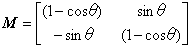
Mの逆行列M-1は簡単に求められます。それは、MtをMの転置行列として、
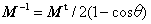
この関係を応用することで、p0を求める関係式を下のように導くことができます。
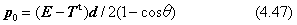
この解p0には、上で説明したように、回転軸方向のベクトルuの成分を持っていません。
次のページ