(1) 局所座標系TAで定義した行列TBを世界座標で表したTに直す。

(2) 世界座標で定義した行列Tを局所座標系TAで定義したTB
に直す。

4.4.5項と4.4.6項では、変換行列が、定義に使った座標系を変えるとどのように変わるかを説明しました。そのときに次のような演算式が表れました。
(1) 局所座標系TAで定義した行列TBを世界座標で表したTに直す。
(2) 世界座標で定義した行列Tを局所座標系TAで定義したTB に直す。
ここで行列TAは、座標系Aを表す行列であって、この座標系を世界座標で見たとき、その三つの座標軸を表すベクトル(u,v,w)が、縦ベクトルの要素になっているとします。したがって、TAの逆行列TA-1は、転置行列TAtに等しくなります。この節は、式(4.27)と(4.29) の表現が、二項積で表すとどのようになるかを説明します。
行列を一般的に表すときは、要素を縦横に並べて表しますが、これは行列の性質を分かりやすくするための手段です。行列を二項積の一次形式で表すと、いくつかの点で便利になります。まず、一般的な説明をするため、縦ベクトルを要素とする行列Tの表し方をいくつか並べます(付録Aを参照のこと)。
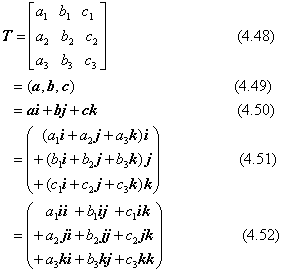
式(4.48) は、一般的な行列の表し方。式(4.49) は縦ベクトルの集合を強調した表し方。式(4.50)は、縦ベクトルに注目し、座標軸を表すベクトルを使って二項積で表した場合。式(4.51) は、ベクトルを座標軸の成分に分解した表し方。最後の式(4.52) は、行列の要素をスカラーとし、座標軸を表すベクトルのみの二項積で表した場合です。このいずれも、数学的には行列Tと同じ働きを持ちます。特に、式(4.52)を簡潔に表現したものが、最初の式(4.48) の右辺の表し方です。いま、座標軸を表すベクトル(i,j,k)の代わりに、別の三つのベクトル(u,v,w)を使った次の表現の可能性を考えます。
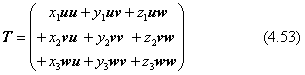
さらに、二項積に乗ずるスカラーだけを取り出した、次の行列を考えます。
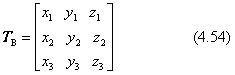
実は、式(4.48)〜(4.53) は、数学的にはすべて同じ行列Tですが、式(4.54) のTBは、Tと同じものではありません。この表し方は、(i,j,k)を使った下の表現と同じです。
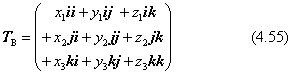
二つの行列TとTBとは本質的に同じものであって、基準に考えている座標軸を(i,j,k)とするか、(u,v,w)とするかの違いであるとします。この4.6節は、式(4.48)から、式(4.55) を求める方法を説明しようということです。
世界座標系(WC)とは、座標軸を表す単位ベクトが(i,j,k)です。新しい局所座標系(LC)を定義するには、別の単位ベクトル(u,v,w)を決めます。この三つのベクトルは、世界座標で見ると、互いに直交した右手系の単位ベクトルであるとします。この条件を満たさない特別の場合については、次の4.6.3項で説明します。いま、局所座標系にいる人になって考えますと、その人の座標系が宇宙の中心で、自分の座標系が(i,j,k)であると考えて、世界座標系の方が特別な座標系に見えます。これが座標変換の原理です。世界座標から見て局所座標系(LC)を定義する行列の表現では、(u,v,w)を縦ベクトルとする3×3行列にまとめて表します。これをTAと書いて、二項積として次のように表します。
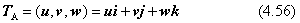
逆行列は、この場合TAの行と列とを入れ替えた転置行列TAtと等しくなります。
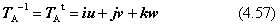
ここで、式(4.53) で仮定されている行列Tを挟むように、形式的に左からTAtを、右からTAを演算させます。
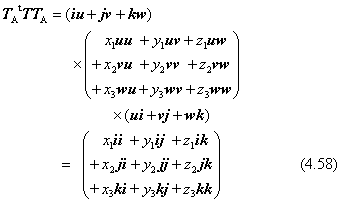
ここで得られた式(4.58)は、前項の式(4.55) と同じです。結局、この4.6節の最初に例示した式(4.54)の座標変換が得られました。
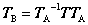
逆変換については式(4.58)の(i,j,k)をそれぞれ(u,v,w)に置き換えることです。これは、TBの左側からTAを、右側からTA-1=TAtを演算させることです。
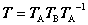
座標変換を理解するには、この章の最初の4.1節で紹介したように、ビデオカメラで撮影した映像を自宅のテレビで見ていることを想像するとよいでしょう。カメラを通して見た世界を我々がテレビで見て、眼の前の現実のように理解することが、局所座標系によって座標変換されたと言います。テレビで見た映像が、普段見ている景色と形も寸法も正しいとき、この座標変換は直交座標変換であると言います。このときは、カメラ座標軸の向きと単位を示す三つのベクトル(u,v,w)が、右手系の互いに直交する単位ベクトルになっています。しかし、すべてはそうでなく、ズーミングなどでは映像の大きさが変化しますし、場合によると、いびつに変形した映像が得られます。この場合には、座標軸を決めるベクトルは、必ずしも単位ベクトルではなく、また、直交性も満足されないであろうし、右手系の位置関係でない場合すら考えられます。
局所座標系を表す行列TAは、式(4.56) と同じように(u,v,w)を縦ベクトルとする行列で与えることができます。しかし、変換させる行列Tの左右から演算させる行列は、TAをそのまま使ってはいけません。演算に使う行列は、TAとTAtに代えて、下に表式を用います。
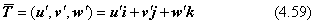
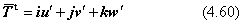
ただし(u',v',w')は、(u,v,w)から次の関係で求めなければなりません。
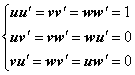
上の関係式は、行列の演算では、下の関係式と同じです。
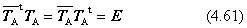
座標変換およびその逆変換は、下のように表されます。注意することは、演算させる行列の種類が異なることです。
