4.2節で、立体図形を拡大もしくは縮小する変換を扱いました。その4.2.7項で、三つの直交する方向ごとに倍率の異なる拡大・縮小をさせる行列を次のように与えました。

ただし、(u,v,w)は、互いに直交する三つの単位ベクトルです。行列Tは、上の定義から明らかなように、対称行列です。この節は、行列Tが与えられて、ベクトル(u,v,w)と、係数λ1、λ2、λ3を求めることであって、4.2.7項の逆問題を扱います。そして、この問題は、線形問題における固有値解析と呼ばれるものです。ここに、(u,v,w)を固有ベクトル、λ1、λ2、λ3を固有値と言います。固有値問題は、4.6節で扱った座標変換の計算でもあって、与えられた対称行列を変換して対角行列に直すことです。座標系を行列TA=(u,v,w)で与えると、固有値の計算は次のようになります。

対称な行列Tの要素を、下に示すような記号σとτを使って示します。このギリシャ文字の記号は、材料力学では応力を表すものとして、常識的に使われている方法です。

ただし、対称行列の条件は、τ21=τ12、τ31=τ13、τ32=τ23です。あるベクトルp=(x,y,z)が固有ベクトルであり、そのときの固有値がφである条件とは、「行列Tとベクトルpを演算させて得られるベクトルが、pをスカラーφ倍したものに等しい」というものです。式に書くと、Tp=φp、すなわち

これを代数式で書くと、

この同次連立方程式において、x、y、zのすべてが 0ではない解が存在するための条件は、係数行列の行列式(デターミナント)が0となる条件を満たすφを求めることです。つまり、

上の式は変数φの3次式であり、代数学の問題として扱うときには、三つの根を大きい順に番号をつけて、λ1、λ2、λ3とする習慣になっています。固有値に属する固有ベクトルを求めるには、式(4.67)の解で得られた固有値の一つを、式(4.66) に代入した連立方程式から求めます。しかし、幾何の問題として固有値と固有ベクトルを求めるときには、固有値の並べ方とベクトルの向きの定義には注意が必要です。これは次項で説明します。
一般的なn次の対称行列の固有値を求める場合の基礎的な知識として、最も単純な2次元の対称行列の固有値解析を説明します。2次元の対称行列は、下に示すように考えます。行列の二つの固有値をλ1、λ2とし、固有ベクトルはu=(u1,u2)、v=(v1,v2)とします。

二つの固有ベクトルu、vは、それぞれ単位ベクトルであって、互いに直交するので、角度θをパラメータとして、x、y座標面の二つの動径ベクトルとすることができます。

これを代入して成分の関係を求めますと、

さらに、三角公式を使って整理すると、

このように式で書くと、式の意味を理解し難いので、これを2次元の(σ、τ)座標系を使って描いたものが図(4.10)です。この表現方法は、弾性体の力学ではモールの(Mohr' circle)と呼ばれ、2次元弾性体の主応力の大きさと向きとを求めるときの説明に使われています。円の半径は0.5(λ1-λ2)、円の中心座標は、σ軸上の0.5(λ1+λ2)です。偏角θの2倍をパラメータとする動径が、この円と交わる座標が(σ1,τ)、(σ2,-τ)となります。
図4.10 モール円による固有値解析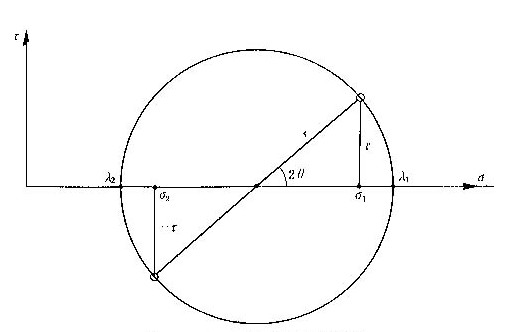
対称な2×2の行列の固有値問題は、上に述べた式に対する逆問題です。つまり(σ1,σ2,τ)が 与えられて、(λ1,λ2,θ) を求めることです。図4.10と式(4.70)とから、円の半径は、

二つの固有値は、

偏角θを求める式は、

ここまでの代数的な説明には、固有値と固有ベクトルの決め方に、いくらか曖昧なところがあります。一般的な約束では、まず、図4.10で例示したσ1>σ2という条件は必ずしも成り立ちません。幾何学的な性質を考えれば、二つの主軸方向を示すベクトル(u,v)の方向は、もとの座標軸の単位ベクトル(i,j)を、なるべく小さな回転角度(-45°<θ<45°)で回転させたいと考えます。これは、式(4.69)で、cosθ>0を条件に決めることです。結局、二つの固有値の大小関係を次のように決めます。
・もし(σ1>σ2)ならば(λ1>λ2)と決め、θを+σ軸方向から測る
・もし(σ1<σ2)ならば(λ1<λ2)と決め、θを-σ軸方向から測る
・ θの符号は、τ(σ1-σ2)の符号に合わせる
4.7.2項で説明した2次の対称行列の固有値解析の方法を繰り返して、一般のn次の対称行列の場合に拡張した方法が、Jacobi法と呼ばれる数値解析の方法です。n次の行列の場合には、仮想のn次元空間を考え、そこに互いに直交するn個の単位ベクトルを考えます。この単位ベクトルを列(縦)ベクトルとする行列をAの記号で表すことにします。

与えられた元の対称行列をTとします。固有値解析は、元の対称行列に座標変換を何回も繰り返し計算をして、対角線以外の要素が0に近づくように直していくことです。最初の対称行列をT0=Tとし、k番めの繰り返し計算で得られた対称行列をTkとしますと、その時の単位ベクトルの行列Akとに下の関係が成り立ちます。

計算の方法は、次のようにします。初期値は、T0=T、A0=E です。ここでの単位行列Eは、対角線要素だけがすべて1、他の要素がすべて0の対角行列です。k番めの行列Tk、Akは、k-1番めの行列Tk-1、Ak-1を補正するように計算します。その方法は、Tk-1の対角線要素のなかで、まだ0ではない要素τij=τjiだけに注目し、そのi番めとj番めの行と列とで構成する2×2の要素に注目します。そして、τij=τji=0となるように座標ベクトルeiとejとを回転させます。その回転行列をHkとします。これは前項の式(4.69)と本質的に同じ処理です。すなわち繰り返し計算(イテレーション)を次のように行います。

行列Hkの成分は、単位行列の変形であって、i番めとj番めの行と列とが下のようになっています。

記号はC=cosθ、S=sinθの意味です。行列Hkは、座標軸のベクトルのうち、eiとejだけを下のように回転させます。

式(4.74)によって、Tkの主対角線以外の要素が実用上十分に0となるまで補正を繰り返しますとTkは、固有値の並んだ対角行列に収束し、Akが固有ベクトルの集合として得られます。この際、固有ベクトルは、すべて互いに直交する単位ベクトルの条件が満足されます。この繰り返し計算では、ある非対角要素τijを0にする計算を行っても、別の繰り返し計算で数値が代入されることがあります。そのため、実用計算では、大きな数値の非対角要素から先に補正し、すべての対角要素が十分に小さくなったところで計算を打ち切ります。このアルゴリズムでライブラリ化されたプログラムでは、固有値の大きい方から順に並べ直して、固有ベクトルもこの順に並べ変えるものが見受けられます。そうすると幾何学的な意義が失われてしまいますので、利用するときには注意が必要です。
次のページ