(1)ベクトルpを、(u,v,w)のベクトル方向の成分に分解します。これは、(u,v,w)が互いに直交する単位ベクトルであるので、pとのスカラー積を求めておきます。
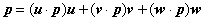
(2) ベクトル(u,v,w)の方向に、(λ1、λ2、λ3)でスカラー倍します。
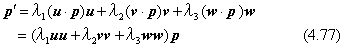
(3) ベクトル(u,v,w)を、それぞれ(a,b,c)で置き換えます。
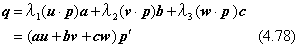
一般的に考えて、3×3行列は、9個の要素から成り立っています。ということは、行列の性質を分類すれば、9種類あるはずです。これまでの各節の説明で扱った行列は、いずれも、要素になにがしかの条件のついた、特殊な行列でした。その特徴は、次のようです。
(1) 図形を回転させる行列: 行列の縦ベクトルが互いに直交する単位ベクトル
(2) 拡大・縮小を行わせる行列: 主対角線に対して対称な行列
図形の回転は、回転軸の向きを与えるベクトルと回転角で定まるので、変数の数は4個です。しかし、ベクトルが単位ベクトルである条件があるので、独立の条件は3個になります。対称な行列では、3個の固有値と三つの固有ベクトルがありますが、固有ベクトルの9個の成分の間には、互いに直交する単位ベクトルという条件が六つあるので、独立な条件は3個に減ります。つまり、一般の3×3行列は、上の2種類の変換を一つの変換行列で行なわせるものです。この行列をTとすると、それを二項積で次のように表すことができます。
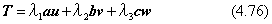
ただし、(a,b,c)と(u,v,w)とは、それぞれが直交する右手系の単位ベクトルであって、(λ1,λ2,λ3)はスカラーです。いま、a=u、 b=v、 c=w のときが、4.7節で論じた対称行列の固有値解析でした。また、λ1=λ2=λ3=1で、u=i、v=j、w=kとしたものが、4.5節で論じた回転を与える行列です。この節では、一般の行列Tが与えられたとして、式(4.76)の右辺のスカラーとベクトルを決定する一般的な方法を解説します。
式(4.76)の右辺で表されている二項積が、ベクトルpを変換させてqを求める演算にどのような役割を持つかを説明しましょう。まず、変換は
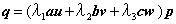
この変換の手順を箇条書きにして説明します。
(1)ベクトルpを、(u,v,w)のベクトル方向の成分に分解します。これは、(u,v,w)が互いに直交する単位ベクトルであるので、pとのスカラー積を求めておきます。
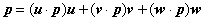
(2) ベクトル(u,v,w)の方向に、(λ1、λ2、λ3)でスカラー倍します。
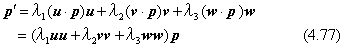
(3) ベクトル(u,v,w)を、それぞれ(a,b,c)で置き換えます。
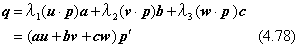
上の手順で、(2)の演算は、対称な行列による拡大縮小変換と同じ意味です。また、(3)の演算は、回転を行わせる変換です。この手順を入れ替えて、回転を先に、拡大縮小を後に行わせると考えることもできます。つまり
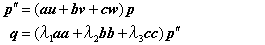
式(4.76) の行列の転置行列をTtとします。これは、式(4.76)の二項積の構成ベクトル(a,b,c)と(u,v,w)の並びを前後入れ換えたものです。
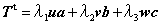
TとTtの積を求めると、対称行列が得られますが、それは、積の順序を換えると2通り得られます。
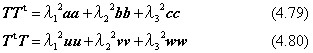
この二つの対称行列は、4.7節で説明した固有値解析を行うことにより、それぞれ独立に固有ベクトル(a,b,c)と(u,v,w)を求めることができます。ここで計算される固有値は、それぞれ2乗した値(λ12、λ22、λ32)で求まります。符号を含めて、(λ1、λ2、λ3) とベクトル(a,b,c)を決定するには、元の行列Tを使って、(u,v,w)との積が下のように得られる関係を用いることができます。
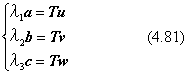
なお、(u,v,w)を決めるにあたっては、右手系の関係を満たすようにベクトルの向きを定義する必要があります。さらに、式(4.81) を使って(λ1、λ2、λ3)の符号を決める場合、(a,b,c)が右手系の関係を満たすようにすることも大切です。
式(4.76) の行列に含まれる純回転の成分を分離したものが、式(4.78) に示されています。これをHで表すことにしましょう。
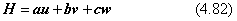
この行列Hは、4.3節で説明した回転を与える行列の性質を満足することを確かめることができます。つまり、この逆行列H-1は、転置行列Htに等しくなります。
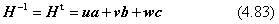
もとの行列に逆の回転を行わせる演算はHtTであり、その結果元の行列は対称行列に変換されます。
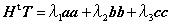
もう一つの積の演算は次のように(u,v,w)に関した対称行列を求めることができます。
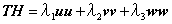
式(4.3) で最初に示した変換式q=Tp+dは、pを与えてqを求める式でした。逆に、qを与えてpを求める変換式が必要になるとき、p=T-1(q-d)の形で計算式を求めたいため、Tの逆行列が必要になります。具体的に数値計算が必要な場合、逆行列の計算テクニックとして種々の方法が提案されています。しかし、多くの数値計算の参考書が触れているように、逆行列の計算は計算誤差を生じやすく、なるべくなら逆行列の計算をさけることを提案しています。この説明は、いくらか誤解されやすい面があります。本当の意味は、T-1を計算しておいて、改めて(q-d)との積の演算をすることを避けることを提案しているのであって、なるべくなら、最初から積のままの形T-1(q-d)で得られるように計算することを薦めているのです。どうしても逆行列を必要とする場合においても、元の行列の性質を十分に理解した上で逆行列を判断することが望まれます。式(4.76)で示した一般的な3×3行列の逆行列は、次の形になります。
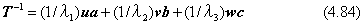
ここで、仮に|λ1|>|λ3 |であるとき、|1/λ3|>|1/λ1|となることに注意しなければなりません。つまり、(λ1、λ2、λ3)の数値の中で、どれかが絶対値で非常に小さくなっているとき、その逆数だけが他の成分よりも極端に大きくなってしまうからです。(λ1、λ2、λ3)の数値の中で、どれか一つでも0に近付くと、逆行列の数値計算ができなくなる理由は、式(4.84) の形を見ればあきらかでしょう。実際に、3×3の行列であっても、元の行列が正則でない場合の例は、4.5.4項の回転の中心を求めるところで、式(4.46)に示しました。数学的な課題は逆行列の問題ですが、数値計算としては2次元の逆行列を応用していることに注目して下さい。
次のページ