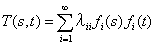この章の最初に示したいくつかの変換式(4.1)〜(4.3)は、二組の変数p=(x,y,z)とq=(x’,y’,z’)との関係をベクトルと行列Tという数学量で表しました。ベクトルp、qそれぞれの三つの成分を空間における座標と考えることで、幾何学的ないくつかの性質を説明してきました。ベクトルという数学量は、大きさと方向とを持った量として扱えますので、かなり具体的なイメージで理解することができます。一方、行列というのは、ベクトルとの演算をして始めてその性質が表れる演算子の性質がありますので、一段上の概念で理解しなければなりません。行列をベクトルの集合したものと考えると、ベクトルの集合を図に描くことができます。その図は行列そのものを具象して表わしているのではありませんが、行列の性質を理解する補助になります。幾何で扱う行列の性質を種々の角度から見たのがこの4章の内容でした。そして、行列の具体的な利用は、座標を変換する下の形であるとして論旨を通しました。
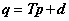
一旦数式化して抽象化がされてしまいますと、幾何の概念を拡張して扱うことができます。これは4.7節の固有値解析で応用しています。そこでは、ベクトルの成分数が3を超えても使われますので、一般のn次元空間という概念が使われます。そこでも、固有ベクトルとは、互いに直交する単位ベクトルであるという概念で使われています。ところが、ベクトルの次元数nの値が大きくなってくると、一組の変数をn個の座標軸ごとの座標値で表わすという考え方が実用的でなくなります。ある変tをパラメータとして、その変数のある区間、例えば(0<t<1)で定義された連続関数f(t)を考え、tのとびとびの座標で離散化した数値の一組(f1,f2,…fn)を便宜的にベクトルと考えるようにします。こうすると、ベクトルの大きさを表す概念に、幾何ベクトルで考えたベクトルの長さという考え方を利用できなくなります。そのため、関数f(t)の二乗平均(幾何平均、RMS: root mean square)の方を、関数f(t)の寸法を測る単位にします。これを関数のノルムといいます。ベクトルの長さはベクトルのノルムともいいますが、これは関数のノルムの1/nで定義することになります。
いま、一つの変数sで表される連続関数p(s)、q(s)、d(s)と、二つの変数s、tで表わされる関数T(s,t)を考えます。ここで、下のように表される積分方程式を考えます。
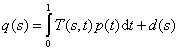
この式は、変換を表す式q=Tp+d と本質的に同じように英字記号を合わせて表現しました。ここで使われた2変数の関数T(s,t)を、グリーン関数ということがあります。一般的な議論をするとき、sとtとを入れ替えて代入したT(s,t)とT(t,s)とは等しくないとします。また、変数sとtの変域も、必ずしも同じではありません。この形式と同じ式は、構造力学では影響線という実用計算式で使われています。橋に自動車などの分布荷重p(t)が作用したときのs点での撓みq(s)を求めるときに、撓みの影響線をT(s,t)と置いてこの積分式の形が使われます。実際の数値計算では、撓みを求める場所をとびとびの点で考え、荷重の方もその点に集中させた集中荷重を考えますので、座標値は離散化した数値の一組で考え、結果的に式の扱いがベクトルと行列の表現になります。変数sとtの変域を別々の区間で考える場合には、関数T(s,t)は行列で言えば矩形行列に対応します。変数sとtの変域の区間が同じであれば、行列で言えば正方行列に対応します。特に、T(s,t)=T(t,s)の関係が成り立てば、これは、対称行列に対応します。
単位行列Eと座標軸を表す単位ベクトルi、j、kは、デルタ関数δ(s,t)に対応します。Eは、s=tの場所だけが1で、他はすべて0となっている特殊な関数ですので、対角線要素が1で他の要素がすべて0である単位行列に相当しています。単位ベクトルの方は、単位行列の一つの行ベクトルまたは列ベクトルですので、2変数のデルタ関数において、ある注目点sを定数とおいてtを変数とした1価関数に相当します。デルタ関数は、代数学的な考え方では説明が難しい概念です。これは、上の積分方程式で使った関数T(s,t)と同じように、積分して使って、始めて意味のある数値が得られるからです。
上の積分方程式を扱うとき、関数をフーリエ級数で表すことがあります。一般的に扱うときは、変数sの区間で定義された関数列を使って、
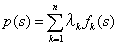
のように表すことが行われます。この関数列fk(s)は、ベクトルの計算で言えば、座標軸以外のベクトルの集合で、例えば
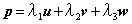
と表すときのu、v、wに相当します。いま三つのベクトル(u,v,w)を互いに直交する単位ベクトルに決めるのと同じように、fk(s)は、ノルムが1の直交関数列になるように決めることがあります。直交性というのは、下で示されるような関係です。
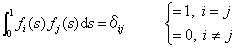
ちなみに、この積分の計算は二つのベクトルの内積の計算に相当しています。
行列を二項積の形で扱うことは、2変数の関数を下のように二組の関数列の積で考えることに対応しているのです。
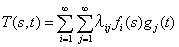
特に、sとtとに関して対称性のある関数T(s,t)が下の式のように表されるときには、対称な行列の固有値解析で得られる表現に対応しています。