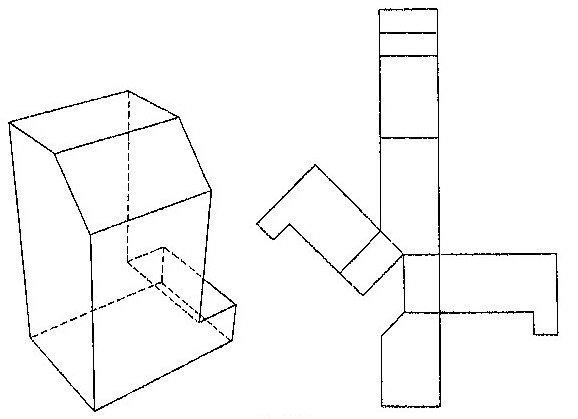
ある平面図形の原図形を、別の作画領域の指定した場所に写したいと考えます。このときの分かりやすい指示方法は、原図を囲む四辺形の枠Aを、写す側の四辺形の枠Bに割り付けるようにして原図全体を伸び縮みさせます。実践的なデザイン作業では、それぞれの四辺形をさらに細かくメッシュに区切って、単純な図形単位ごとに原図の細部を写していきます。この方法を数学的に扱うことが変換です。四辺形の枠や、その内部をメッシュに区切ることが座標系の定義をしていることになります。
普通に行われる平面図形の変換は、原図を囲む方の四辺形Aを正方形または矩形とし、図を貼り付ける側の四辺形Bも相似の図形を考えます。原図側から見れば、図の貼りつけは写す側の領域への平行移動、拡大または縮小、回転、場合によると裏返し(鏡像)などの変換がされたことになります。原図形を相似に写すことの他に、原図形に変形を加えたいことがあります。この変形には二種類あって、その特徴は次のようになります。
図5.1 平面図形の種々の変換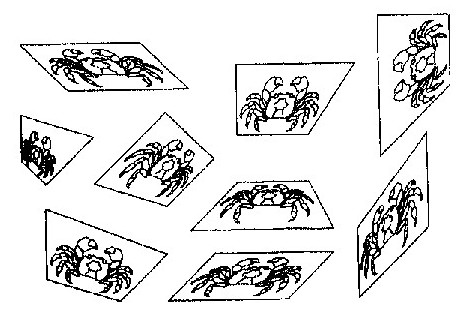
(1)正方形が一般的な平行四辺形になる変形:
この変形は、縦方向と横方向とで拡大または縮小の倍率が異なる変換です。例えば、正方形が矩形になるような変形です。正方形が菱形になる変形は、正方形の二つの対角線方向で拡大または縮小の倍率が異なる変換です。(2)相対する二辺の平行性がなくなる変形:
この変形は、正方形を斜めの向きから写真に撮ったときに得られる図形が代表的なものです。これが射影変換です。射影変換を一般的に扱う場合には、写真で得られた図形に対して、さらに上の(1)の変換が加わって変形されます。射影変換は次の5.3節で説明します。
アフィン変換とは、図形を変形させないで平行移動や回転をさせることに加えて、上の変形の種類の分類(1)を合わせた変換の総称です。図形の左右が反転する変換は、変形の特殊な場合であって、二つの方向の拡大または縮小の倍率が一方で+、もう一方で−の符号になった場合に起こります。この変換の数学的方法は、前の第4章で説明した変換行列を2次元図形に応用したものです。式(4.1)〜(4.3)は下のように簡単になります。
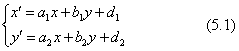
形式的に下のような表現も使います。
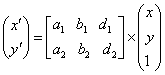
ここで現れる2×3の矩形行列を平面図形の代数的な意味での変換行列と言います。幾何学的には、変換の主要部分の2×2の正方行列が回転と変形とを処理し、残りが平行移動の成分を表しますので、下のように分けて表記します。
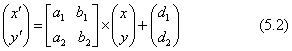
この式を、記号を使って下のような代数式で表します。これは式(4.3)と同じですが中身は2次元の扱いで用います。

具体的に平面図形のアフィン変換の数値計算をするには、次のような手続きが必要です。まず原図の各点を表すために座標系を定義します。この座標系を使って、原図を囲む四辺形枠Aの3頂点の座標を与えます。この3点は、四辺形の左下隅、右下、左上です。データとしてはこれらの座標6成分です。図を理解しやすくするため、データとしては左下隅の頂点座標(位置ベクトル)と、四辺形の枠の向きを示すように、その頂点を起点として右下の頂点までのベクトル、同じく左上の頂点までのベクトルを描きます。図形を写す側についても作図領域の座標系を決め、貼り付ける四辺形枠Bを決めます。このデータも原図に対応させた三つのベクトルです。アフィン変換では、図形同士の相対的な位置の対応に3頂点のデータを使いますので、原理的には、三角形を三角形に対応させる変換です。四辺形の枠を考えるのは、枠の外側に図がはみ出ないようにするためであって、ウインドウの枠と同様に、グラフィックスの処理におけるクリッピング範囲を決めるデータとしても利用します。
アフィン変換は、式(5.2)で使われる6個の定数a1、a2、b1、b2、d1、d2を決めれば計算できます。代数学の問題にすると、二組の四辺形枠のそれぞれ6個のデータを使って6元連立1次方程式を立てて解きます。しかし、幾何の問題としてとらえると、もっとスマートにアフィン変換を考えることができます。それは、次のように解釈します。原図の枠の四辺形Aも、写す側の四辺形Bも、基礎となるデータが同じです。それは世界座標の原点を起点とした単位の正方形であるとします。この単位の正方形を、別々に変換をして原図側と写す側との四辺形にしたと考えます。
四辺形のデータは平面図形の2×3の変換行列Mの成分(a,b,d)であるように整理して考えます。つまり、dが四辺形の左下隅の頂点座標で、a、bが二辺の向きと長さとを与えるベクトルとします。二組の四辺形のデータを記号MA、MBとします。アフィン変換Mは、原図内に在る点の座標を一旦単位正方形内のデータに直し(逆の変換)、改めて写す側の四辺形の枠の中におとします(正の変換)。Mは矩形行列ですので、理論的な意味では逆行列を定義できませんが、記号式を使って概念的にこの変換を表現すると下のように表すことができます。
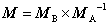
具体的な数値計算に使う表現は第4章で説明しましたが、この概念的な代数式をG-BASICでは次のように書けばよいように設計してあります。
M=MB*REV(MA)
ここに、M,MA,MBは、2次元の変換行列として前もって宣言された変数記号で、成分数は6個です。MA、 MBの中身のデータはLET文で代入します。REVはG-BASICの組み込み関数で、引き数の内容をその型で逆の形式に変換させます。引き数が変換行列であれば、その変換行列の逆変換行列が求められるようになっています。
平面図形のアフィン変換は、基本的には点の座標を変換行列で変換させる式(5.1)で行わせます。G-BASICの表現では、変換行列に積の演算子をつけて、変換させたい幾何要素を右から演算させればよいように設計してあります。平行移動と、単純な拡大または縮小は、わざわざ変換行列を求めて演算させなくても、単純にベクトルの加算とスカラー倍をすれば処理できるようになっています。回転を行わせる変換と、鏡像変換とには、組み込み関数MROT、MIRRを使います。変換させる方のデータ型で、線分は両端の点をデータの構成要素にしてありますので、図形の変換に直接利用することができます。しかし、直線の場合には、直線上の二点を変換した後で、データを標準のデータ構造に直します。2次元の変換行列の型は、図形的には座標軸を表す2本の線分で構成されていますので、変換が演算できます。円・矩形の型は、平行移動と拡大・縮小が眼に見える変換として処理演算されますが、回転処理が無効で結果として外接図形が得られます。
すでに第4章で説明したように、3次元(立体)図形の拡大・縮小・回転・変形・移動などを計算するとき、変換行列の形で考えるのが便利であるとして、種々の有用な式を説明しておきました。その出発となった式が(4.1)です。形式的に行列の表現にしたのが下の式です。
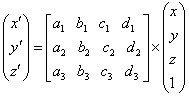
ここで表れる3×4の矩形行列のことを代数的な変換行列と言い、G-BASICではこれを3次元の変換行列の一つのデータ型で扱うようにしています。2次元図形の場合、この矩形行列による変換をアフィン変換と呼ぶので、立体図形の変換の場合もアフィン変換と呼ぶことにします。
実践的に平面図形をアフィン変換させる場合には、原図形の平行四辺形枠を、写す場所の平行四辺形枠に「嵌め込む」という処理を考えました。立体図形のアフィン変換では、平行六面体から平行六面体への嵌め込みを考えて、3×4行列の12個の定数を決定します。これは、平行六面体の8つの頂点の中、4頂点の座標で考えます。これは、一つの頂点座標を原点とし、そこを起点とした三辺について、向きと長さとを与える三つのベクトルとで与えます。このようにして決めた二組の局所座標系をデータとすれば、立体図形のアフィン変換の変換行列Mは式(5.4)と全く同じように計算することができます。ただしデータ型は3次元の変換行列で定義した変数です。
回転を行わせる変換の変換行列は4.5節で解説しました。そこで導いた公式を利用するため、組み込み関数TROT、XROTが準備してあります。また、鏡像変換を行わせるために、組み込み関数TMIRRが準備したあります。変換させる方のデータ型について言えば、例えば、面では、面上に三点を考え、その三点を変換し、この三点を通る面になるようにデータ型の標準化が内部的に行われます。
ここまでの説明は抽象的でしたので、やや具体的な処理について解説します。それはCADにおいて二つの幾何モデルが接するような移動をさせたい、という条件をどう解決するかを例として考えることにします。
まず平面図形の場合を考えます。二つの多角形図形A、Bがあって、指定した辺で二つの多角形が接するように、一方の多角形Aを変形させないで回転と移動とをさせるような変換行列を求めたいと考えます。この場合の条件は、回転と移動をする多角形Aの側と、接続する方の多角形Bの側とで同じ長さの辺を考え、その辺が重なるように回転と移動とをさせます。辺の定義はそれぞれ二つの頂点座標で考えます。この条件は2次元の変換行列の6成分の中、四つの条件を決めることです。変形しないという条件が残りの二つの条件を与えます。
図5.2 平面図形の接続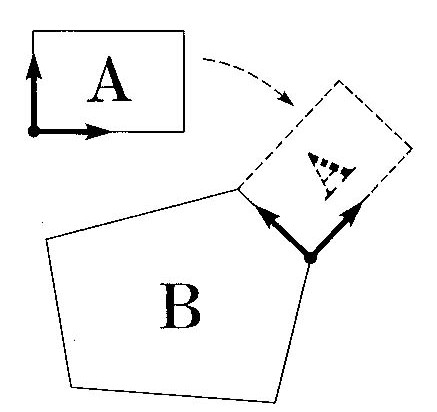
変換行列が座標系を定義する形式でもあるので、接続させたい二つの多角形モデルA、Bの中にそれぞれ子の局所座標系を決めます。その場所は、接続させる辺とします。原点の位置を辺の一つの頂点の座標とします。一つの座標軸の向きと長さとを与えるベクトルは、原点からもう一つの頂点へと向く有向ベクトルとします。もう一つの座標軸を与えるベクトルは最初の座標軸を定義するベクトルと直交させ、同じ長さに決めます。このようにして決めた二組の局所座標系を、記号MA、MBと書くことにします。ここでMAは移動させる方の座標系、MBは移動先の方の座標系とします。図形の接続は、MAを移動させてMBに重ねることです。こうして式(5.4)を使って変換行列を求めて、モデルAの座標を変換させれば、指定した辺を介して二つのモデルが接します。
立体図形の場合、二つの多面体の指定した面で二つの多面体A、Bが接するように一方の多面体Aを変形させないで移動させるような変換行列を求めることを考えます。接触させる二つの面を指定するには、それぞれの面を表どうしでピッタリ合わせるように、鏡に写せば合同になるように、一方の三角形は裏向きに考えます。二つの三角形が重なるように一方の多面体Aに回転と移動とをさせます。3次元の変換行列の12成分のうち、九つを決める条件がこの三角形の三点の座標です。三角形の一つの頂点を原点とし、その原点を起点とした二辺を二つの座標軸にします。もう一つの座標軸は、先の二つの座標軸と直交させるようにベクトル積で求めます。変換行列を考えるときの考え方は、平面図形の接続の場合と本質的に同じ方法です。接続を考える面に合同な局所座標系を定義することに変えれば、式(5.4)がそのまま応用できます。
一般的に図形を接続させるときの条件は、双方の接続させる場所に貼リ合わせ用の図形を考え、その二つを重ね合わせることです。この図形の定義に、子の局所座標系を考えます。この場合の局所座標系は、必ずしも世界座標系のコピーの条件になっていなくても構いません。座標軸の長さが異なっていても、また斜交座標でもよいのです。さらに一般的な場合、重ね合わせる三角形が合同でない場合に拡張しても構いません。このとき、移動させる側の図形は一般的な平行六面体に変形する変換を含みます。
サイコロのように全体の構造が平面で構成されている立体図形では、面ごとに固有の平面図形が書き込まれることがあります。この立体図形を透視図に描き、見えている面に描いてある図形を透視変換したいと考えます。これは、平面図形を、一旦3次元の平面に貼りこんで、その3次元の図形データから透視変換をさせるという二度の変換で処理することができます。この最初の変換が、ここで説明する変換です。
平面図形を考える場合、この平面図形を囲む矩形の領域を考えます。多面体の面についても矩形の領域を定義します。平面図形の方の座標系に(x,y)座標を使っているとした場合、この座標面に垂直なz座標軸をダミーとして加えこの矩形の定義を3次元の座標定義の行列に直します。多面体の側での矩形領域の定義は、前節と同じです。図形貼りこみの変換行列は式(5.4)を使います。ただし変換のデータを与えるとき、平面図形のデータは(x,y)座標だけを使い、z軸の値を常に0と代入します。
図5.3 平面図形の立体図形への貼りこみ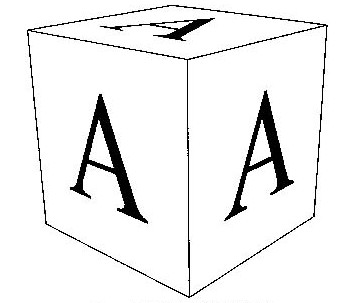
サイコロを例に上げますと、展開図というのは、多面体の各面ごとの正投影を接続辺で順に繋いだ図形です。この処理は、各面の正投影を求める変換に続けて、二つの隣接した面を辺で繋ぐ処理との二つから成り立っています。立体的なデータを持った多面体の面の実形を求めるには、対象とする面に垂直な視線を持つように視点座標系への座標変換をしなければなりません。投影図は、座標変換をした上で、奥行き方向のデータを捨てて2次元の図形データに直したものです。この変換では、得られる投影図の向きをどう決めるかが悩ましい問題になります。サイコロのような六面体の展開図の標準的な投影図の配置は附録Cに示しました。サイコロを机の上に置く置き方は24通りありますので、それぞれについて、回転を与える3×3の行列がみな異なっています。適切な回転行列を選ぶのは人間の感性による判断が必要です。
図5.4 展開図