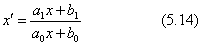
ある平面図形の原図を囲む四辺形の枠が矩形であっても、写す側の四辺形の枠がその矩形と相似ではないような変換が考えられます。この変換は、四辺形の形の性質に関係しています。結論からいうと、矩形が一般的な平行四辺形に変形するような変換と、それ以外の任意の凸四辺形に変形する変換とに分けることができます。前者がアフィン変換、後者を一般的な射影変換といいます。射影変換は数学的な用語であって、図学的には中心投影変換に相当します。アフィン変換はこれに対して図学的には平行投影変換になります。アフィン変換で扱うのは平行四辺形枠を別の平行四辺形枠に割り付ける変換です。正方形・矩形・ひし形は、平行四辺形の特別な形状です。これらの四辺形に共通する性質は、二組の対辺がそれぞれ平行線であることです。一方、射影変換では、対辺が必ずしも平行ではない一般的な四辺形に変換されます。都会の建物を写した写真では当たり前として見ていますが、ビルの壁面や窓の線は平行ではありません。ただし、射影変換でも、正面から写真を撮る場合のように、四辺形の二組の対辺がそれぞれ平行である場合を含みますので、一般的な射影変換はアフィン変換をも含めて扱うことができます。
図5.5 平面図形の射影変換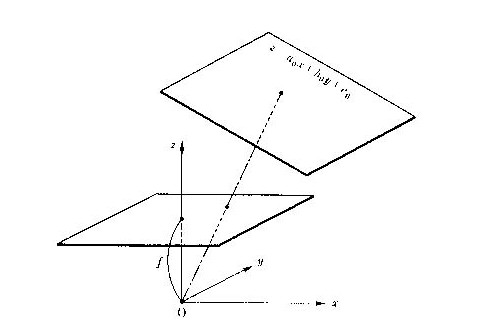
2次元図形の射影変換の原理を説明するには、ビルの壁面のような平面領域に描かれた図形を斜めから中心投影原理のカメラで撮影したような透視投影図を考えるのが分かりやすいでしょう。ただし、幾何学的な3次元の座標系では、図5.5のように中心投影の視点を原点とした視点座標系を考えます。3次元空間で、図形が描かれている平面と、透視投影面とは平行ではありません。投影面は(x,y)座標面に平行で、カメラの焦点距離fに相等するz=fの位置に置きます。原図が描かれている面はこの3次元空間の中での傾いた平面であって、面のz座標が z=a0x+b0y+c0 で与えられるとします。傾いた面に描かれている原図の各点を表す座標は、傾いた面の中に考えた平面座標系ではなく、この視点座標系の(x、y)座標で表します。原点(視点)と傾いた面上の座標とを結ぶ直線が投影面と交わる所の座標を考えます。そうすると、原図の座標(x,y)は、投影面では下の式で示した座標(x',y')に変換されます。
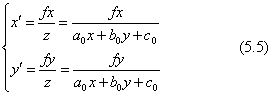
射影変換の特徴は、分母に(x,y)の1次式があることです。これによって遠くの図形が小さく、近くの図形が大きく投影されます。また、この1次式は面の式を与えています。視点座標系の中に置かれた傾いた面上に描かれている図形は、別の原図からそこに写されたと考え、そこへの図形の複写は式(5.1)のアフィン変換が適用されるとしますと、射影変換の一般式が下のように得られます。ただし、焦点距離fによるスカラー倍は式の係数に含めて考えることにします;
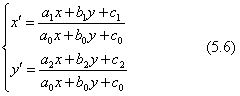
上の式で使われる九つの係数(a0,a1,a2,b0,b1,b2,c0,c1,c2)を決めれば図形の射影変換が計算できます。ただし、式(5.6)は分子分母をスカラーで通分できますから、独立した未知数は8個になります。この8個の係数を定める方法は、原図側と写す側と、四辺形の4頂点を上の式に代入して、8元連立方程式を解くのが代数的な解き方です。原図側の四辺形を矩形として、写される側の四辺形は原則として凸四辺形でなければなりません。
平面図形の射影変換を実用的に計算するには、原図側と写す側とにそれぞれ四辺形の枠A、Bを考えます。枠Aが枠Bにちょうどはまるようにする変換式を作ります。データは、四辺形を一周する頂点座標の並びです。四辺形を一周する頂点の並びは同じ順でなければなりません。例えば、四辺形を一周する頂点の番号並びを1、2、3、4の順で考えるとして、原図側と写される側の四辺形の頂点の並びが1、3、2、4のように捩じれることは許されません。ただし、1、4、3、2のように逆回りの対応づけは許されます。この場合には図形を裏返す処理を含みます。
変換に使用する原図側の四辺形枠Aには、計算しやすいように配置した単純な矩形を考えます。図5.6に、標準の射影変換に使う四辺形を示してあります。この四辺形を一般的な四辺形に貼りつけるように射影変換する計算式は式(5.6)です。そこで使われる九つの係数(a0,a1,a2,b0,b1,b2,c0,c1,c2)の計算式を付録Eにまとめておきました。任意の形状をした四辺形Aから別の任意の形状の四辺形Bに貼り付ける変換は、四辺形Aを一旦標準の矩形に戻すような逆変換をして、改めてこの矩形から四辺形Bに貼り付けるように二度の変換をさせます。この考え方は、アフィン変換で説明したのと同じです。射影変換の逆変換は後の節で解説しますが、数値計算用の実用式は、付録Eに付けました。
図5.6 二次元射影変換の代数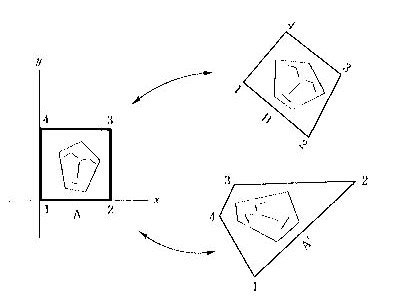
二次元図形の射影変換では、射影の原理を説明するために3次元の空間を考え、そこに二つの平面を考えました。この考え方を一般化して、代数学的に抽象化したn次元図形の射影変換を説明するときには、(n+1)次元の仮想の空間を考え、n次元図形はその仮想空間の仮想平面(超平面)に描かれているとします。説明を簡単にするため、n=3の立体図形の射影変換で説明しましょう。変換の一般式は式(5.5)を3次元に拡張した式です。
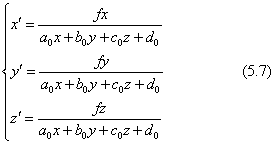
射影変換では、直線は直線に変換されても、平行な二直線は変換後必ずしも平行にはなりません。立体的な射影変換においては、変換前の平面は変換後も平面である、という条件になり、立体的な射影変換の一つの重要な性質です。式(5.7)の意味づけには、仮想の4次元空間(x,y,z,w)を考えています。この空間に二つの超平面があります。一つは(x,y,z)座標面に平行で、w=fの位置にある仮想の投影面です。もう一つの面は(x,y,z,w)の空間にある傾いた仮想の面で、そこに図形が描かれています。その面の面方程式が式(5.7)の分母を与えています。この超平面の式は下のように表されます。
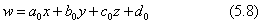
傾いた方の超平面には図形が描かれていますが、別の原図からそこに図形がアフィン変換されて描き込まれたと考えた変換式が一般的な射影変換の式になり下のように表されます。
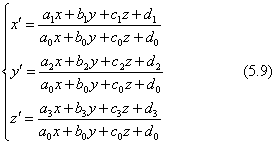
3次元図形の射影変換では、正立方体(正六面体)から、各面が一般的な四辺形に変形するような一般的な六面体への変換を考えます。しかしちょっとした注意が必要です。式(5.9)は係数が16個ありますが、この式が分数式ですので代数的な未知数は15個です。つまり、頂点5個の対応で考えなければなりません。六面体は頂点が8個ありますから、その中の5点を選び、どの4点も一平面上にあってはならない、という条件を満たす必要があります。幾何学的にこの条件を満たすような5頂点の選び方は、例えば、長さが単位の正六面体の一つの頂点を原点に合わせたとして、下のような座標で示される点になります。
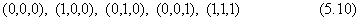
ここで除外している3頂点の座標は、(0,1,1)、 (1,0,1)、(1,1,0)です(図5.7)。
3次元のアフィン変換では平行六面体から平行六面体への嵌め込みでしたので、データは4頂点が必要でした。したがって変換は四面体から四面体への嵌め込みと考えることができます。3次元図形の射影変換を一般的に扱う場合には、各面が三角形である六面体同士での変換の対応を考えます。この六面体は底面を共通にした二つの三角錐(四面体)を繋いだ形になっています。このような六面体は実際の形状設計では滅多に使いませんので、立体図形の造形デザインに射影変換を意図的に応用することはあまりありませんでした。上の基本六面体を使う射影変換の実用計算式を付録Eにまとめました。
図5.7 三次元射影変換で使う基本立体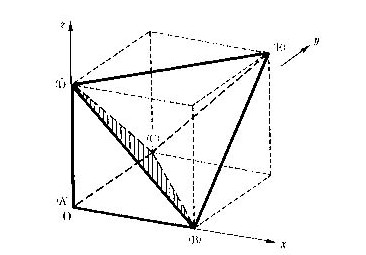
3次元の射影変換を応用する場合には、式(5.7)に示した基本的な射影変換を考えるのがよいでしょう。2次元図形の射影変換の式(5.5)を導いた考え方を応用して、立体図形の射影変換のあらましを想像することができます。式(5.7)で、四つの係数(a0,b0,c0,d0)とfの選び方が射影変換による立体図形の変形の性質を支配します。対象となる立体図形は、アフィン変換で考えたように、この立体図形を包み込むような直方体の箱の寸法を考えると便利でしょう。考え方を分かりやすくするため、変換の手順を箇条書きにまとめます。
(1) 変換元の立体図形は、原点を中心として縦・横・高さが2h×2h×2hの正六面体の座標空間で考えます。
(2) 4次元の仮想空間で、正六面体中心の置かれている場所のw座標がd0>0、投影面のw座標をf0>0とします。
(3) 変換前の正六面体の寸法と、変換後の六面体の寸法とを大体同じにしたいときは、d0≒f0とします。変換後の六面体の寸法を小さくしたいときはd0>f0に選びます。
(4) 視点と正六面体中心との距離をw軸で測った寸法がd0です。正六面体の一辺の寸法hよりも大きく選ぶのがよいでしょう(d0>h)。
(5) 中心投影図との類推で、h/d0が見かけの視角を与えます。h/d00が小さくなると、平行投影つまり立体図形のアフィン変換に近付きます。
(6) 正六面体の寸法の範囲で、超平面を表す式(5.8)のwはw>0でなければなりません。w=0は超平面がw軸と交わることを意味していて、変換した方の図形の座標が無限遠に延びてしまいます。変換図形の座標が有限である条件は;w1= d0-(|a0|+|b0|+|c0|)h>0
(7) 変換された六面体の辺の長さは伸び縮みします。伸びる方では一辺が大体f/w1倍になります。縮む辺は、f/(2d0-w1)倍になります。伸び縮みの差が大きい方が射影変換の特徴を強調できる変換です。
(8) 変換元の正六面体は、仮想の(x,y,z,0)の空間にあって、それを式(5.8)の超平面に写して考えました。正六面体の各辺は座標軸に平行に置いてありますが、これを任意の向きになるように、その中心で六面体を回転させることを考えます。すると、一般的な射影変換の式(5.9)の形を考えたことになります。この場合、式(5.9)の分母にあたる超平面の式は変えません。
立体図形の簡単な応用例として、正六面体から台形への変換を挙げます。台形というのは下が広く、上が狭い形です。式(5.7)において、z軸に関する係数だけについて下のような射影変換を考えます。
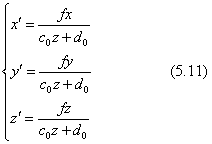
ここで、一辺が2の正六面体を変換します。係数として f=d0=5、 c0=1 とします。すると、六面体の2×2の天板は、1.67×1.67の正方形で高さがz=1からz=0.87に低くなります。また2×2の底板は2.5×2.5の正方形で、高さがz=-1よりも下がってz=-1.25に移ります。つまり、この3次元の射影変換で、2×2×2の正六面体は、底辺が2.5×2.5、天板が1.67×1.67、高さ2.12の台形に変形されました。変形の対象となった正六面体の中に任意の立体形状を嵌め込んで考えれば、この台形の射影変換による変形のあらましが想像できるでしょう。例えば球形は卵形に変形できます。
図5.8 立体図形の台形への射影変換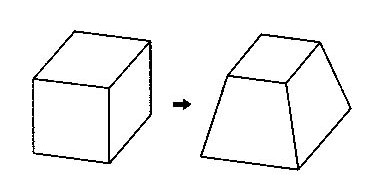
ついでですから、平面図形の射影変換の式(5.5)の応用として、2×2の正方形から台形への射影変換を例示しましょう。この場合の式は、y軸方向だけを考えますので、式(5.5)を下のような式で考えます。
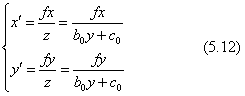
係数として、f=c0=5、b0=1とします。この射影変換は、上の正六面体を横から見た図形に変換されたものと等しいので、底辺が2.5上辺が1.67、高さ2.12の台形に変形されます。
図5.9 矩形から台形への二次元射影変換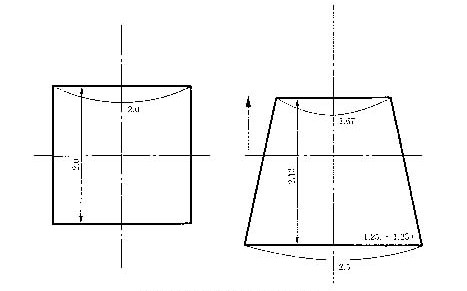
図5.5の射影変換では、図形が描かれている平面と透視投影面との二つの面がありました。この二つの面の立場を逆にして、透視投影面の図形を斜めになった方の面に逆投影する変換が逆変換になります。この場合の元の射影変換の式は、平面図形では式(5.6)、立体図形では式(5.7)で考えます。2次元の射影変換の場合を含めた一般的な説明のため、3次元の射影変換の式(5.7)の変換式を再掲し、逆変換式(5.13)と並べて示します。
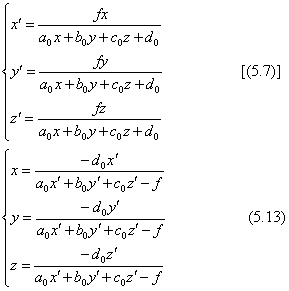
この二組の式は全く同じ形式をしていて、fと-d0とを単純に入れ替えただけの係数表現になっています。式(5.7)の形をした射影変換の式は、図学的な原理に基づいて求めた射影変換の式(5.5)を概念的に3次元の射影変換に拡張したものですが、逆変換の表現式と比べてみれば分かるように、式の形は非常にきれいにまとまっています。一般的な射影変換式(5.9)は、幾何学的な意義をあまり考慮していない代数式ですので、この逆変換式を求めるのはかなりの難問になってしまいます。
逆変換を求める場合には、まず、分子の方の表現を式(5.7)のような標準形にするような中間変数(x”,y”,z”)を考えます。これは、(x’,y’,z’)から(x”,y”,z”)への変換はアフィン変換です。標準形に直せば(x”,y”,z”)と(x,y,z)との逆変換が簡単に求められます。そこで、先のアフィン変換の逆変換を求めて、中間変数(x”,y”,z”)を(x',y',z')に戻します。解が代数的に求められるかどうかは、アフィン変換の解があるかどうかで判断できます。
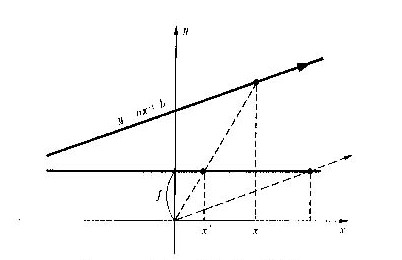
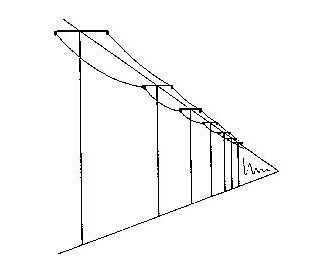
一直線の鉄道線路をやや斜めから眺めたとき、電車の架線を支える等間隔の電柱が、近くは高さが大きく間隔が広く見え、遠くに行くに従って高さが低く、間隔が密に見えます(図5.10)。これを1次元の射影変換の例と考えることができます。等間隔に並んでいる電柱の座標xが、投影面では不等間隔の座標値x'に変換されます。1次元の一般的な射影変換を表す代数式は、2次元の射影変換の式(5.6)を元にして下のような形に表されます。
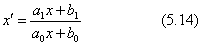
上の式(5.14)の変数x'とxとの関係をグラフに描けば、図5.11に例示したように、x=-b0/a0の直線と、x'=a1/a0の直線とを漸近線とした双曲線のグラフになります。式(5.14)から、xをx'から計算する逆変換の式(5.16)が簡単に求められます。式(5.14)のグラフと式(5.15)のグラフとは、グラフの縦軸と横軸とを入れ換えただけです。
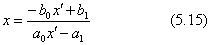
式(5.14)の係数を少し変えて、式(5.5)または式(5.7)式と形式を揃えた下の式(5.16)は、図学的に見た1次元の射影変換の標準形です。
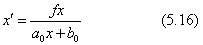
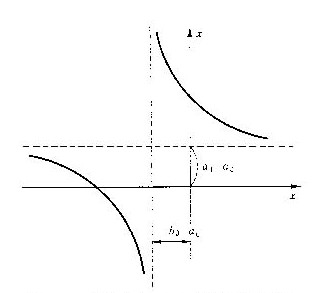
上の式の分母は、(x,y)平面座標系で考えたy=a0x+b0の直線式を与えます。この直線上の点(x,y)と原点(0,0)とを結ぶ直線が、y軸に平行な直線y=fと交わる点を求めると、そのx座標がx'になります(図5.12)。式(5.16)において、xに等間隔で座標値を代入して分母を+∞または−∞にしていくと、x'の座標値が増加または減少していきますが、その増分または減分は順に小さくなり、分母が+∞ではx'⇒f/a0に収斂して行きます。この座標点が、遠近法の用語で消点(vanishing point)になります。
式(5.13)の形において係数(a0,a1,b0,b1)を決めれば一般的な射影変換を表します。この場合には2次元の(x,y)座標系とは別に、直線上に異なった直線座標を決めたことになっています。1次元の射影変換の四つの係数を決めるためには、式(5.13)が分数式ですので、仮にb0=1と仮定して、残りの3係数を決めます。独立な係数は3個になりますので、この未知数を求める条件は、xについて(x1,x2,x3)の3点、x'について(x'1,x'2,x'3)の対応を考えて3元連立方程式を解けば求めることができます。計算の条件として、(x1,x2,x3)と(x'1,x'2,x'3)との数値の並びは昇順または降順でなければなりません。
図5.12 一次元の射影変換の原理図