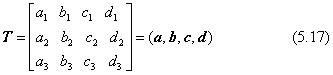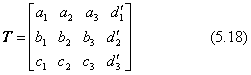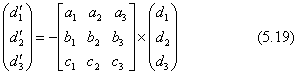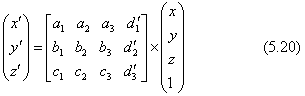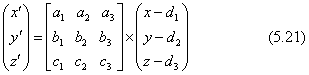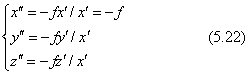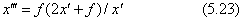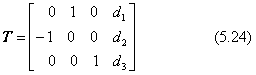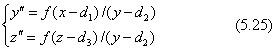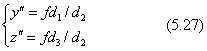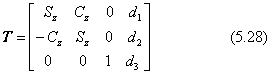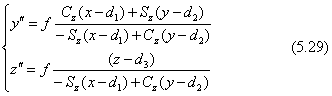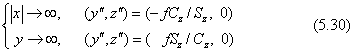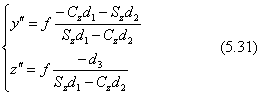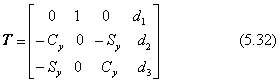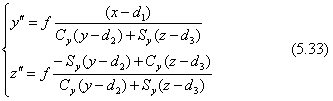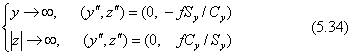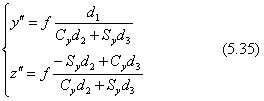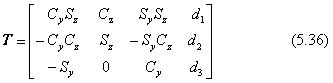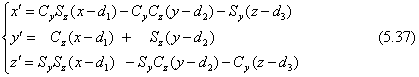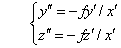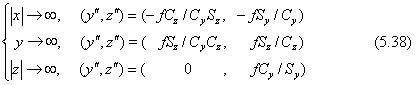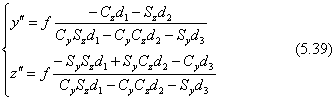5.4 透視図の数学
前のページ;
次のページ
5.4.1 透視図法の考え方
立体図形の幾何モデルをコンピュータグラフィックスの応用で描くことは、ごくありふれたコンピュータ技術になってきました。しかし、この技術を自分で納得がいくように勉強しようとなると、種々の専門的な分野が入り組んでいるので、簡単に全体を理解することが容易ではありません。実践的なコンピュータグラフィックスの技術を覚えることの努力の大半は、ハードウェアとソフトウェアの使い方に費やされてしまいます。そのため、基本となる投影変換の数学については、説明が行き届かないのが普通でした。実を言うと、この節にくるまでの各章があって、やっと透視図の説明に入る準備ができたと言えるのです。透視図の数学に必要な概念は、座標系の理解・座標変換の考え方・変換行列の数学・射影変換の数学です。これから説明する透視図法は5.3節で説明した射影変換の応用です。しかし図学的な約束と合わせるために、用語や定義が部分的に変わります。最初に透視図を作るための道具立てを説明します。
図5.13 透視図法の原理を説明したイラスト

まず座標系の約束から始めます。透視図を考えるには、右手系の「世界座標系」の中に「対象物」とそれを写す仮想の「カメラ」を考えます。対象物とカメラそれぞれは固有の「局所座標系」を持っています。局所座標系は、世界座標系と図形的に相似です。カメラについては「カメラ座標系」と呼びますが、図学的には「視点座標系」と言います。カメラはレンズとフィルム面があり、これが図学的には「視点」と「投影面」に対応します。カメラ座標系は、原点をレンズの中央に置き、座標軸の取り方は、前章の図4.8のように約束します。座標系の定義は恣意的ですので、ここでの定義は他の参考書とは違うかも知れません。この章の説明で注意しておくことは、普通にカメラを構えてファインダを通して対象物を見るとき、レンズの軸方向をx軸とし、その正の向きがカメラを構えている人の手前方向と約束していることです。つまり、対象物はカメラ座標系では-x軸の領域にあります。実際のカメラではフィルム面はカメラのx軸ではx=fにあって像が倒立で写りますが、図学的な透視投影面と整合させるため、「透視投影面」をx=-fに置きます。ここでfは仮想の焦点距離です。投影面に平面座標系を考えますが、カメラ座標系のyz座標をそのまま当てはめます。前項の5.3節で解説した3次元射影変換の座標定義とは異なっていることに注意します。
世界座標の中でカメラの位置とその向きとを決めることは、カメラ座標系を定義することです。これを3×4の「座標系を定義する行列」で与えます。これは、代数的には3×4の「変換行列」です。カメラの向きは、変換行列の最初の3列のベクトルで表されます。これは、最初のカメラ座標軸の向きを世界座標系の座標軸と平行に揃えていた状態から、パン・スイング・ティルトの三回の回転で向きを変えた、とした計算になります。この計算の詳細は、4.4.7項「カメラの操作を表す変換」で説明してあります。実際にカメラを構えて写真を撮ることを想像すれば分かるように、カメラのファインダを覗いて被写体である対象物を視野に納める場合には、パンとスイングの二回の処理で済ませます。ティルトは、被写体を視野に収めたまま、レンズの光軸(x軸)回りに回転させることですので、ティルト処理は省略します。この約束は投影面座標系(yz)を決めるとき、y軸を世界座標系で常に水平に置くことです。この条件では、カメラで見た世界座標系の水平線が、投影面のyz座標系では常に水平な直線として写ります。
カメラの向きを決める場合、被写体である対象物(の一点)とカメラ光軸とを結ぶ向きがカメラのx軸の向きと一致することを利用すると、カメラを回転させる考え方よりもカメラ座標系をずっと簡単に定義することができます。カメラのx、y、z座標軸の方向を表す単位ベクトルを(a,b,c)とすると、これは3×4の行列の最初の3列の単位ベクトルです。ベクトルaは、対象物からカメラ向かう向きのベクトルを単位ベクトルに直します。ベクトルbは、aと直交し、xy座標面に平行です。ベクトルcは上向きです。(a,b,c)を右手系の単位ベクトルにすればよいのです。カメラの位置はdで与え、3×4の行列の4番目のベクトルとします。
透視投影面は、フィルム面と同じように矩形の領域を考えます。この矩形の中心をレンズの光軸が通るとして、ここを原点とした2次元のyz投影面座標系を考えます。この矩形領域が透視図法のウインドウです。ウインドウの矩形枠の定義は、カメラで言えばフィルム面の矩形寸法を定義することになります。フィルムは任意に引き延ばしてプリントされますので、理論上のカメラは焦点距離を1とし、焦点距離fはプリントするときの倍率と考えることができます。また、現実に焦点距離fを持った大型のカメラを考え、密着プリントの寸法がそのまま図として使えると考えることもできます。焦点距離1のカメラでフィルムの横幅の寸法をTH2とすると、TH2はレンズの視角(ラジアン)にほぼ等しくなります。通常の標準カメラを考えるときはTH2=0.7くらいですが、ワイドレンズではTH2>1.0になります(表2.2、図2.2参照)。コンピュータグラフィックスの矩形の作画領域には種々の縦横比(aspect ratio)があります(表2.3参照)。その矩形領域の横幅だけに注目し、横幅一杯になるようにフィルムを引き伸ばして貼り込むとすることで、フィルムの縦の寸法を決めます。このように仮定すると、fの距離にある投影面のウインドウ枠の座標は、左右にy=-0.5fTH2、y=+0.5fTH2となります。
特殊なカメラでは、レンズをフィルム面と平行に動かせるものがあって、レンズの光軸がフィルムの矩形領域の中央に来ないような写真が撮影できます。これは「あおり」という撮影技術で、建築物の写真を撮るときによく利用されます。実際の写真でもフィルムを部分的に引き伸ばしてプリントすれば、レンズ中心は写真の中央からずれます。差し当たって、このような特殊な処理は考えないことにします。以上で透視変換の道具立てが整いました。
5.4.2 カメラ座標系への変換
透視図にしたい対象物の座標は世界座標で与えられているとします。もし対象物の各部の座標がこの図形の局所座標系で与えられているなら、世界座標に変換した座標値をあらかじめ計算しておきます。透視変換には、世界座標で与えられた座標値を、カメラ座標系で見た座標値に直す「座標変換」をしなければなりません。これはカメラ座標系の3×4行列の逆変換に相当する変換行列を求める問題になります。代数的な逆変換行列の計算方法は4.1節に説明しました。カメラ座標系の座標軸を表すベクトル(a,b,c)は右手系の単位ベクトルとして定義してあります。すると、この3×3行列部分の逆行列は、成分の行と列とを入れ替えた転置行列になりますので、式(4.5)を使って逆変換を容易に求めることができます。数式の約束を以下に並べます。
(1) カメラ座標系:
カメラのx、y、z軸の向きを表す単位ベクトル(a,b,c)と、カメラの位置ベクトルdとを縦ベクトル成分とする3×4の変換行列。
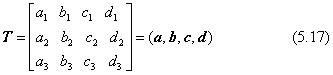
(2) 対象物の世界座標をカメラ座標系に直す変換行列:
上記の3×4の行列Tに対して、逆変換を表す3×4変換行列を下のTWとします。この行列において、最初の3×3の成分はTの同じ場所の成分の行と列とを入れ替えたものになっています。
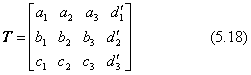
ただし(d'1,d'2,d'3)は、TWの最初の3×3の正方行列部分とベクトルdとの積で求めます。
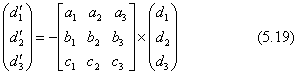
(3) 対象物の世界座標(x,y,z)をカメラ座標系の座標値(x',y',z')に直す計算は上の変換行列を使います。
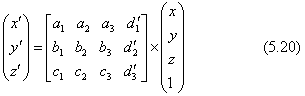
上の式と同じ結果が得られますが、3×3の成分だけを使った下の式も便利に使えます。
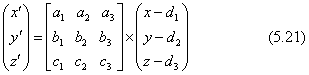
5.4.3 透視変換と射影変換
視点からfの距離に置いた投影面は、カメラ座標系ではx'=-fにあります。対象物の座標(x,y,z)と原点(視点)とを結ぶ視線が投影面と交わる点をカメラ座標系で測ります。
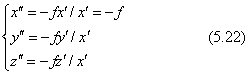
ここで計算された(y”,z”)の座標値が透視図としての2次元座標になります。式にはマイナス(-)の符号が付いていますが、対象物をカメラでみたときのx'座標が常に負の領域にあるためです。分子と分母とには世界座標系の(x,y,z)の1次式を使うと、式の形式は前節の式(5.9)に示した3次元の射影変換と同じ表現になることが分かります。ただし上の透視変換はx”が定数になっていますので、3次元から2次元への変換であって、純粋の意味での3次元の射影変換ではありません。その理由は、(x”,y”,z”)から(x、y、z)の座標に戻す逆変換が計算できないからです。3次元の射影変換の形式にするには、式(5.22)のx”を下の式に変えます。
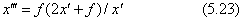
このように(x',y',z')から(x'",y",z")への変換を考えますと、3次元の射影変換になります。透視図は(y",z")だけを使いますが、x'"は3次元に射影変換された図形の奥行き座標を与えます。実際の透視図を描くときにはx'"を必要としませんが、立体図形の隠れ線や隠れ面の消去をしたいときには、この式(5.23)を利用して視点からの奥行きの座標を比較して、どちらが手前にあるかの判定に使います。
5.4.4 一点透視図
テレビ塔の展望台のような高い位置から方眼状に整理された町並みを見下ろすと、道路やビルの外壁の延長線が無限遠で一点に収束しているように見えます。透視図の用語では、これを消点と言います。また無限に遠いところは水平線が見えます。コンピュータグラフィックスでは、方眼状の線が引かれた地形を透視変換して作図した図をよく眼にします。透視図を手書きで作図するときには、下書きにこのような座標線の透視図が使われます。座標線の透視図は、世界座標系の座標軸とカメラ座標系の座標軸との相対的な角度差によって、図学的には3種類に分類します。これを一点透視図、二点透視図、三点透視図(one-point-、 two-point-、 three-point- perspective projection)と言います。この名称は、座標線の消点が投影図上で現れる数からきています。ただし、消点は、描かれている作図領域の中に見えなくて、領域の外にある場合も少なくありません。このことが手書きで透視図を作成するときの用器画技法を難しくしている原因となっています。
実用的に一点・二点・三点透視図を扱うときには、世界がよく見えるようなカメラ位置を考えた実用計算式を提案しておくのがよいでしょう。最初、カメラの座標軸の向きを世界座標系の座標軸と平行に置いた状態を基準に置きます。世界を見渡すことができるように、カメラは世界座標の原点が視野に入るようにセットバックして考え、世界座標系のy軸が手前から向こう側に向く向きになるように合わせます。このモデルは、机の上に世界座標を考えると理解しやすいでしょう。机の上に原点があって、x軸が右手方向、y軸が手前から向こう側へ、z軸を高さ方向に考えます。机の上にある対象物を正面から眺めるようにカメラを構えます。このときのカメラ座標系を世界座標で表すと、式(5.17)が下の式で表されます。
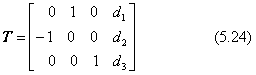
この変換行列の最初の3×3の成分は、付録BとCとを参照して確認して下さい。これは、カメラを世界座標系と一致させた状態から、z軸回りにγ=-90度回転させた向きを表しています。カメラの座標軸と世界座標の座標軸とが平行になるのは、視軸の選び方に関係していて、上の式を含めて実用的には4通り考えられますが、この節ではごく常識的な向きとして、世界座標の+y方向を見る向きで説明します。このように、カメラの座標軸が世界座標軸と平行に置いた状態での透視図を一点透視図と言います。
ベクトル(d1,d2,d3)は、世界座標の中でのカメラの位置です。世界座標の原点が視野に入るようにするためには、d2<0に選びます。地表から高い位置に視点がないと(x、y)座標面が見えませんから、d3>0に選びます。この状態での透視図を一点透視図と言います。透視図の座標(y",z")は下の式です。
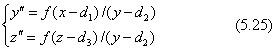
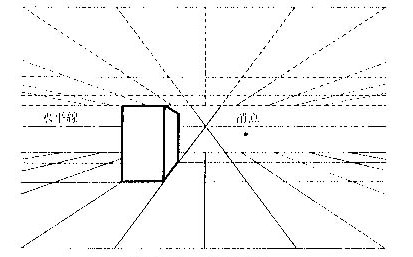
消点は、y→∞になったところの透視図上の位置です。一点透視図では、消点の座標は原点と一致します。すなわち、

一点透視図では、世界座標の中で>y軸に平行な直線はすべて画面中央の消点に向かいます。またx軸に平行な直線はすべて水平線と平行になり、z軸に平行な直線はすべて平行な垂直線になります。つまり、世界座標でy軸に垂直な面の図形は相似形に投影されます。一点透視図は原理的に単純ですので、マンガなどでは立体感を出す背景の描き込みによく利用されています。しかし、奥行き寸法の扱いは図法的に見て正しくない例が多く見受けられます。なお、世界座標の原点の位置は透視図では次の座標です。
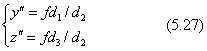
図5.14 一点透視図法
5.4.5 二点透視図(水平方向)
前項で一点透視図を撮影するように構えたカメラを、カメラの鉛直軸(z'軸)を回転軸として左右に振ります。これをパンと言います。世界座標でz軸に平行な直線は、透視図でも垂直な線として投影されますが、x軸に平行な線は投影図では平行でなくなります。パンさせる回転の正の向きはz'軸の正の向きを向いて右回りと約束しますので、カメラを持って左回りに回る角度γをパンの正の角度とします。前節で紹介した一点透視図のカメラの向きは、世界座標系と合わせた状態から-90度分パンした向きになっていました。ここでのパンの角度は、-90度分をオフセットして、0から測るとします。左にカメラを振ると、世界座標の+y軸の消点が透視画面上で右に移動し、画面の左に-x軸の消点が現れます。カメラを右回りにパンすると、反対に画面の右に+x軸の消点が現れます。ただし、パンの角度が小さい場合には、消点は透視画面の枠の外に出ています。角度γでパンしたとき、カメラ座標系を表す式(5.17)は次のようになります。
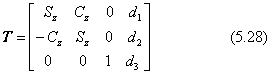
ただし、Sz=sinγ、Cz=cosγ(角度は-90度分をオフセットしました)
透視図の座標(y",z")は下の式で得られます。
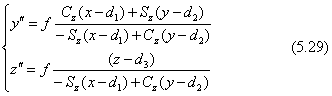
投影図上でのx軸とy軸の消点は下の式です。ただしγの正負によって、x軸の座標軸の向きは-x軸か+x軸かの消点の座標になります。その意味を下の式で|x|と書きました。二つの消点は水平線にあって、そのz"座標は0です。
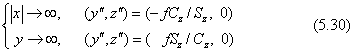
投影図上に写る世界座標の原点は、
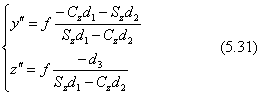
図5.15 二点透視図法
5.4.6 二点透視図(垂直方向)
一点透視図を撮影するように世界座標の+y軸方向を向いて水平に構えたカメラを、左右ではなく、上下に首を振るように動かすことをスイングさせると言います。スイングの角度βは、回転軸がカメラのy'軸になりますので、上を向くように回転させる向きを正の角度とします。スイングさせると、水平線が上下します。また高層ビルを見上げるようなカメラ操作になりますので、高さ方向の線が上で狭くなり、世界座標のy軸の消点とともにz軸の消点が現れ、二点透視図が得られます。この場合の二点透視図はあまり実用されることはありませんが、次節の三点透視図の特殊な場合になります。角度βでスイングしたとき、カメラ座標系を表す式(5.17)は次のようになります。
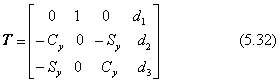
ただし、Sy=sinβ、Cy=cosβです。透視図の座標(y",z")は下の式で得られます。
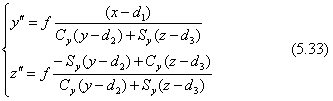
投影図上でのy軸とz軸の消点は下の式です。ただしγの正負によって、x軸の座標軸の向きは-x軸か+x軸かの消点の座標になります。二つの消点は、透視図の中央の垂直線の上に並び、そのy”座標の値は0です。
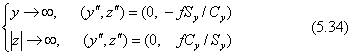
投影図上に写る世界座標の原点は
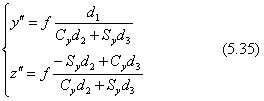
5.4.7 三点透視図
カメラを、パンに続けてスイングさせると三点透視図が得られます。消点が三つ現れるのでこの呼び名が使われます。カメラ座標系を表す式は、式(5.28)と式(5.32)とを合成して次のように表されます。
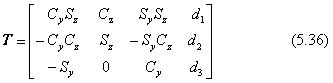
ただし、Sy=sinβ、Cy=cosβ、Sz=sinγ、Cz=cosγ(角度γは-90度をオフセットしました)。透視図の座標(y",z")を直接書くと式が長くなりますので、まず、世界座標(x,y,z)からカメラ座標(x',y',z')に座標変換します。
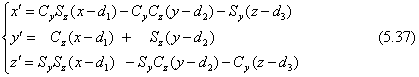
透視図の座標(y",z")は式(5.22)ですが再掲します。
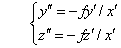
図5.16 三点透視図法
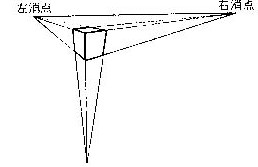
投影図上でのx軸、y軸、z軸の消点は下の式です。角度γの正負によって、x軸の座標軸の向きは-x軸か+x軸かの消点の座標になります。その意味を下の式で|x|と書きました。角度βの場合も同じですので、z軸については|z|と書いてあります。なお、x軸とy軸との消点は同じz”座標ですが、これが水平線の投影図上の位置になります。
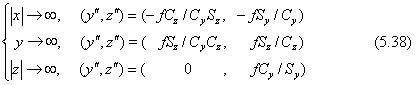
投影図上に写る世界座標の原点は
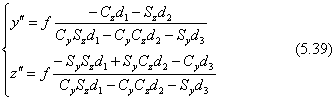
5.4.8 透視図の逆問題
対象物、例えば建物を撮影した写真があるとき、この写真を写したカメラの位置、対象物を視野に入れた向き、写真の引き伸ばしの倍率を求めたいことがあります。これを透視変換の逆問題と呼ぶことにします。この解析の最も専門的な応用が写真測量(photogrammetry)です。写真測量の解析はここではしませんが、コンピュータグラフィックスに応用する例にモンタージュパースペクティブがあります。ある景観の中に、これから建設しようとする建造物の透視図を、あたかも完成したように貼りこむ技術です。この場合には、実際に写真を写した場所の幾何学的なデータを使って建造物の透視図を作り、写真と合成させます。現実感を出すためには絵心のある専門家の助けを借りて修飾するのですが、図法的に正確な形状の透視図が必要になります。このときに透視図の逆問題がでてきます。
透視図を作成するときに何が必要であったかを振り返ってみれば、数学的な問題の背景が分かってきます。
(1) まず、世界座標系を考えなければなりません。写真に写っている対象物の中から、いくつかの注目点を選び、その世界座標(x,y,z)が必要です。いくつの注目点がデータとして必要になるかは後で吟味します。
(2) この注目点について、写真上での2次元座標(y",z")を測ります。記号の約束は透視図を作成したときと同じにしました。一つの注目点は(x,y,z)を含めて5個の数値の一組がデータとして必要です。
(3) 2次元座標系を決めるときは、仮に写真の中央を原点として測りますが、このとき四つの未知数を仮定しなければなりません。それは、
① 写真の引き伸ばしの倍率:f
② カメラレンズの理論的な光軸が、写真中央から逸れていると仮定した座標:(y0",z0")
③ カメラを構えて頭を傾ける(ティルト)ときの角度:α(この影響は、水平線が写真の中で、ある角度を持って写っている場合です。)
(4) 世界座標の中でのカメラの位置と方向は、式(5.16)の3×4の行列で求めなければなりませんが、12個の成分のうち、6個が未知数としての数です。残りの6個の条件は最初の3×3行列が右手系の直交する三つの単位ベクトルでなければならない条件で求めます。6個の未知数の内訳は、
④カメラの世界座標の中での位置ベクトル:(d1,d2,d3)
⑤カメラのパン・スイング・ティルトの角度:(γ、β、α)ただし、角度αは上記の③と同じです。
以上で、数学的には九つの未知数があることが分かりました。これを解くためには、式(5.21)の投影変換に使った(y",z")を計算する二つの式に複数の注目点のデータを代入した条件式を作り、それを解くことになります。九つという未知数の数は半端ですが、これが透視図逆問題の微妙な所です。実際の数値計算をするとき、(2)の写真座標(y0",z0")と、(5)で挙げたパン・スイングの角度(γ、β)の微少な変化との区別を付け難いところがあります。そこで、いくつかの条件を簡単にした場合の、カメラの位置決めの条件を吟味して見ましょう。
(i) 注目点が一つしかない場合;カメラの位置(d1,d2,d3)とfとは分かっていなければなりません。y0"=z0"=α=0と仮定します。求めるのは、パンとスイングの角度(γ、β)の二つです。
(ii) 注目点が二つの場合;何通りかの仮定が考えられます。fが分かっているカメラを使って、ある長さの線分を一定の視野角に収めるようなカメラの位置を考えると、カメラが取り得る位置は、線分に対する円周角一定の円上になります。そのため、実用的な判断は、カメラ位置を決めておいて、(γ、β、α)とfとの四つを計算します。fが与えられている場合には、被写体からカメラまでの距離を変えることになります。
(iii) 注目点が三つの場合には、九つの未知数のうち、三つを仮定すれば残りを決めることができます。それは、y0"=z0"=0の条件と、fを最初から与えておくことです。写真測量の場合には、写真の精度が高いので、写真上に座標が分かっている三点を写し込むように撮影します。ただし、解析に使う座標のデータに誤差があると、計算結果に大きな誤差を発生させます。
注目点が四点以上になると、与えられた条件から解析的に正確な解を数値計算で求めることが難しくなります。この理由は、投影図を求める計算式が分数式であるため、連立1次方程式を解くような線形演算ができないからです。これを解決するには最小自乗法を応用して、誤差を補正しながら繰り返し計算(iteration)をすることです。また、この方法を使うと、データの点数が多ければ多い程、信頼性の高い結果を計算できます。
図5.17 モンタージュパースペクティブ
次のページ