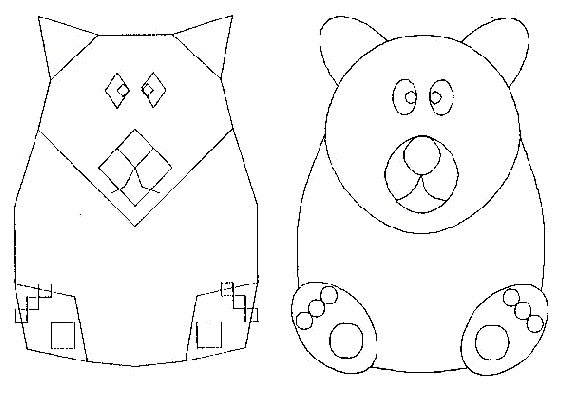
工業製品で曲線を扱う場合、円・楕円・放物線を採用することが多いものです。これらは、単純ですが幾何学的な美しさを持っています。これらに双曲線を含め、数学的にはまとめて二次曲線といいます。コンピュータグラフィックスで滑らかな曲線を描く場合、二次曲線を組み合わせると幾何学的な造形に見え、前項で扱った三次曲線は自由曲線のイメージになります。
コンピュータグラフィックスで二次曲線を描く場合には、曲線の描き始めの点r1と描き終わりの点r3と、もう一点、中間に制御点r >2を決め、ラグランジュ補間を応用して下のようなベクトルの一時形式にまとめるのが実用的です。
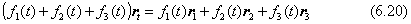
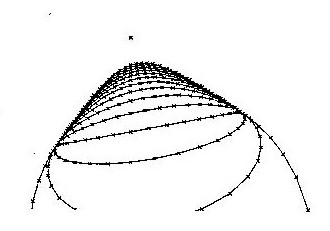
ここで、t=0は曲線の始点を、t=1は曲線の終点を表し、tに(0,1) 間の値を代入すれば中間の点の位置を表すとします。このような表現にしておくと、平面曲線だけでなく、立体的な位置関係にある曲線を表す場合でも応用がききます。f1(t),f2(t),f3(t)はtの関数ですが、付録Gに実用式を整理して示しました。一つの計算式は、r1 >,r2,r3の三角形の二辺に内接する二次曲線(図6.9)、もう一つは三点を順に結ぶ二次曲線で、r2 での曲線の接線が底辺に平行になる条件で与えてあります(図6.10)。この曲線には一つのパラメータaが使われていて、aの値によって曲線の性質が楕円・放物線・双曲線になります。円は楕円の特殊な場合として描けます。楕円を描かせるグラフィックスのユーティリティは、楕円に外接する平行四辺形をデータとして与える仕様が多いのは、このアルゴリズムを応用しているからです。この章の始めに触れたように、円や楕円はsin,cosなどの正弦関数を使はなくても描けます。
ラグランジュ補間は、曲面の補間にも応用できます。考え方は2方向の曲線ラグランジュ補間を組み合わせたものです。計算式は付録Gにまとめました。
図6.9 三角形に内接する2次曲線

10 REM ==== QUADRATIC CURVE ROUNDING A CORNER OF A TRIANGLE =====
20 DEF2PT P : DEF2ED E : CLS
30 LET P1,P2,P3=-20,-20,0,10,30,-10
40 FOR A=3 TO -3.5 STEP -0.5
50 P0=P1
60 FOR T=0 TO 1.01 STEP 0.05
70 S1=(1-T)*(1-T) : S2=T*(2+A)*(1-T) : S3=T*T
80 SN=1/(S1+S2+S3)
90 PP=(S1*P1+S2*P2+S3*P3)/(S1+S2+S3)
100 E=P0 @ PP : P0=PP
110 NEXT T
120 NEXT A
130 END
図6.10 三点を通る二次曲線

10 REM ==== QUADRATIC CURVE GENERATOR THROUGH 3 POINTS =====
20 DEF2PT P : DEF2ED E : CLS
30 LET P1,P2,P3=-20,-20,0,10,30,-10
40 FOR A=3 TO -4 STEP -0.5
50 P0=P1
60 FOR T=0 TO 1.01 STEP 0.05
70 S1=(1-T)*(1-T-T) : S2=T*(4+A)*(1-T) : S3=T*(T+T-1)
80 SN=1/(S1+S2+S3)
90 PP=(S1*P1+S2*P2+S3*P3)/(S1+S2+S3)
100 E=P0 @ PP : P0=PP
110 NEXT T
120 NEXT A
130 END
図6.11 二次曲線で描いたイラスト
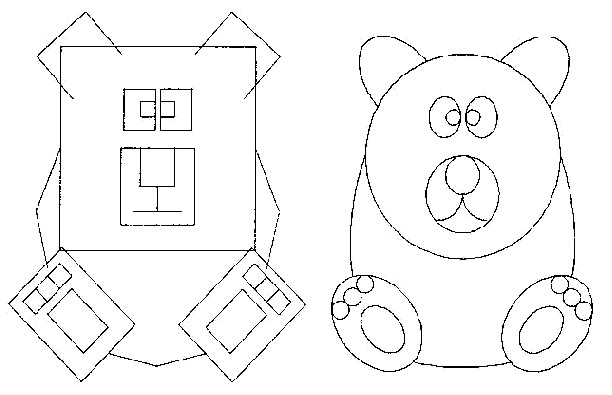
図6.12 三次曲線で描いたイラスト