二点間の距離を求めるためには、その二点の座標をデータとして与えます。データは、二点の位置ベクトルp1=(x1,y1,z1)、p2=(x2,y2,z2)とします。距離は、常識的には下のように計算します。
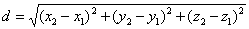
普通、距離は正の数値ですが、距離を座標に転用するときは符号を考えるか、右や左などの言葉を添えてトポロジー的な区別をつけます。さらに、長さと言う場合には、多角形や曲線に沿って距離を測る場合を含みます。この場合の長さの計算が、数値計算の問題になります。例えば、楕円の周長の計算は、簡単なように見えますが、数値計算が厄介な問題の一つです。6.4節で説明したクロソイド曲線の計算においても、弧長と弦長との補正を工夫してあります。
数学式で距離の計算には平方根の表式が現れます。電卓などで平方根は簡単に計算ができますので、手計算で平方根の計算方法を教えることは、ほとんどなくなりました。平方根の計算はプログラム言語では標準の組込み関数として準備されていますが、加減算の計算に比べて数十倍のステップ数がかかります。したがって、長さの計算が大量に必要になる処理では、計算に時間が掛かり過ぎる原因になります。そのため、距離を比較する目的に使う計算では、平方根の計算を省くようにアルゴリズムを工夫します。一つの例が、俗称で言うマンハッタン距離(Manhattan distance)です。ニューヨークのマンハッタン地区は、街路が整然と方眼状になっていますので、ある地点から別の地点までの距離は、物理的な直線距離ではなく、街路に沿った東西方向と南北方向の移動距離の和になります。これは数式で表すと座標の絶対値の和で距離を計算することです。
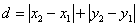
いま、2点間の距離が充分に小さくなって、ある微小距離ε以内にあれば同一点であると判定したいとき、マンハッタン距離を使います。2点間の距離が、ある長さ以上離れていることを確認する場合でも、予備的にマンハッタン距離で判定して、平方根の計算をなるべく省きます。
次のページ