1次モーメントGx
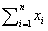
1次モーメントGy
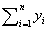
1次モーメントGz
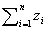
重心(平均)x0
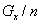
重心(平均)y0
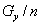
重心(平均)z0
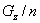
二次モーメントrxx
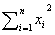
二次モーメントryy
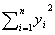
二次モーメントrzz
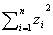
相関モーメントrxy
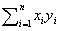
相関モーメントryz
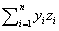
相関モーメントrzx
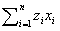
全部でn個ある数値の一組x1,x2,…xnを考えます。この数値の性質を理解したいときに、平均値とか分散などの統計的な数値を計算します。今、この数値に、n個の点の座標pi=(xi,yi,zi), i=1…nの成分を考えて、これを使って点群の統計量を計算します。このとき、次のような幾何学的な定数の呼び名が使われます。
|
1次モーメントGx |
|
|
1次モーメントGy |
|
|
1次モーメントGz |
|
|
重心(平均)x0 |
|
|
重心(平均)y0 |
|
|
重心(平均)z0 |
|
|
二次モーメントrxx |
|
|
二次モーメントryy |
|
|
二次モーメントrzz |
|
|
相関モーメントrxy |
|
|
相関モーメントryz |
|
|
相関モーメントrzx |
|
上の表式をベクトルとマトリックスとを使って下のように書き表すことにします。
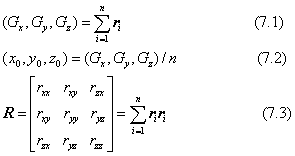
式(7.3)の右辺は、同じベクトルriを二つ使った二項積の和です。したがって、行列Rは、計算の定義から明らかなように、対称行列です。
力学では、上の点群それぞれを単位の質量を持った質点と考えて、質点の集合体を質点系といいます。質点系の運動を考えるとき、重心の位置に全体の質量が集中し、二次モーメントRを持った物体と考えます。具体的な立体図形に応用するとき、点群の個々を微小な立体要素dV=dxdydzに考えて、和の代わりに全体の図形領域で積分します。点の数nの代わりに、全体の体積Vを使った表現が次の式です。
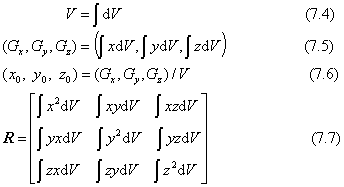
平面図形に応用するときは、上の表現で、z=0, dz=1として、微小面要素をdA=dxdyとします。これは厚みが1の立体図形と考えることもできます。
式(7.7)の行列Rを求めるとき、座標の原点を重心に移した値で求め、これをその図形の二次モーメントと呼びます。その計算式は、下のようになります。
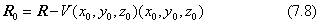
ただし、上の式の右辺の第2項は、重心の位置ベクトルの二項積です。二次モーメントは、座標軸を考えると6成分ありますが、これを対称行列で一まとめで考えます。そうすると、この対称行列は主軸変換によって対角線行列で表すことができます。これを下のように表します。
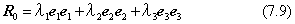
ここで、e1,e2,e3は、主軸の方向を示す単位ベクトルであり、λ1,λ2,λ3は、各軸方向の二次モーメントです。工業設計では、立体図形についての二次モーメントの計算はあまりおこなわれませんが、平面図形については多くの設計資料が作られています。
平面図形の二次モーメントは、式(7.7)、(7.8)、(7.9)でzの項を省いて二次元の行列で考えます。例えば、細長い鋼材は、断面の形状による呼び名をつけて、種々の寸法のL形鋼、I形鋼、H形鋼などが製造されています。これらの材料カタログには、断面の主要寸法・重心位置・断面積・断面二次モーメントなどが載っています。L形鋼など、非対称の断面部材では、主軸の方向がx軸、またはy軸からの角度で表示され、主軸についての慣性モーメントも載っています。
細長い断面の部材は曲げに抵抗するように使われますので、座標軸方向の二次モーメントが大きいほど、その軸と直交する方向の軸回りに曲げ剛度が大きくなります。回転軸を考えるときには、この二次モーメントを慣性モーメントとも言います。図形を表す平面座標系において、x軸回りの慣性モーメントはryyになることに注意します。平面図形の二次モーメントはx軸とy軸との2方向ありますが、これを足したrxx+ryyの値は座標軸の向きの定義に無関係に一定値になります。これは、平面図形の重心に垂直な回転軸(z軸)を通したときの、回転に対するの慣性モーメントになります。
平面図形の二次モーメントrxx,ryyと面積Aとをもとに計算した、下に示す値を、その図形の座標軸方向の二次半径、または慣性半径といいます。
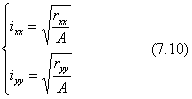
式の形は、平面図形のx軸とy軸それぞれの方向で、面積要素の幾何平均値を表します。これは、統計処理における標準偏差σに相当する値です。構造物の柱の設計においては、柱の高さhとixx(もしくはiyyのどちらか小さい方)の値を使ったh/ixxを柱の細長比といいます。細長比が大きい柱はヒョロ長く、小さな柱はズングリした性質を表します。力学では、慣性モーメントは材料の比重を重みにして計算しますが、構造力学では材料の弾性係数の比を重みにして、異なった材料で複合された部材断面の二次モーメントを計算します。構造物の設計は、部材の形と寸法とを決める作業です。この場合、デザイナが形状を考え、エンジニアが部材断面の幾何学的係数を計算するような共同作業のできることが一つの理想です。
次のページ