コンピュータが使えなかった時代の設計では、あまり自由な形状をデザインすると、図形の幾何学的定数を計算することができませんでした。面積の計算を例にすると、複雑な形状をいくつかの矩形の要素に分け、残った部分を三角形の要素として計算しました。つまり、面積計算の公式では矩形と三角形の場合しか利用しませんでした。それも、要素は、底辺の向きと高さとを座標軸方向に揃えるように分割しました。コンピュータが利用できるようになって、複雑な図形であっても、図形を囲む多角形の頂点座標が与えられれば、面積計算を始め、種々の幾何学的定数の計算ができるようになりました。ただし、頂点の座標を具体的に準備するには、デジタイザを使って図形から直接読み取る場合と、幾何モデリングの手法から間接的に求める、などがあります。
コンピュータで図形の定数を計算させるとき、図形をすべて三角形要素の集合で扱います。計算に使う式は付録Hにまとめました。三角形のデータを与えるとき、頂点の座標を位置ベクトルで表すようにしておくと、三次元空間にある三角形の場合にも応用できます。頂点番号の並びは、領域を左に見るような順番で与えます。逆回りの順番では面積が負の値で計算されますので、図形の内側に穴がある場合にも、穴の面積を差し引いて計算ができます。この性質を応用したのが任意図形の面積計算です。図形の内側でも外側でもよいのですが、任意の基準点を決め、図形を構成する辺とで作られる三角形の面積を、符号付きで計算すれば図形の面積が計算できます。辺の向きは、図形を左に見る向きを正の向きと約束します。面積を機械的な装置で求めるプラニメータは、この計算原理を巧妙に使っています。
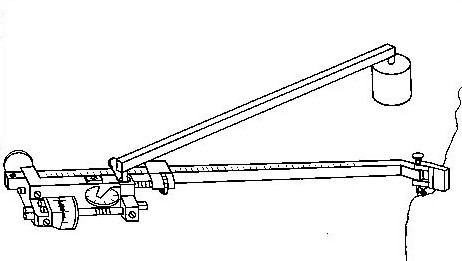
図7.1 プラニメータ