立体的な形状をコンピュータで扱うようにすることは、平面図形を扱う場合に比べると開発は遅れていました。この理由の大半は、コンピュータの能力で制限されていて、大量のデータを扱うことができなかったからです。16ビットのパーソナルコンピュータの環境では、サイコロのような六面体の幾何モデルを、高々70個程度しか扱えないような情けない状態でした。パーソナルコンピュータでも32ビットの環境になって、幾何モデル制作の束縛がほとんどなくなりました。
中身の詰まった立体的な形状をコンピュータで扱うとき、この幾何モデルをソリッドモデルといいます。幾何学的に矛盾のない処理をさせるためには、多面体でモデルを作る(モデリング)必要があります。この場合、多面体を構成する多角形の頂点座標が一平面に載っていなければなりません。この条件は、数値計算では誤差の影響を受け易いので、表面をすべて三角形で覆うようなモデルが利用されます。そうすると、ソリッドモデルの構成要素が四面体になりますから、四面体の幾何定数の計算が必要です(付録H)。ここではその利用方法について簡単に解説をしておきます。
まず、中身のつまったソリッドモデルを多面体で考えます。多面体の表面は多角形とします。内部に空洞があれば、その内側も表面です。多角形は、辺で囲んで構成しますが、データとしては頂点の座標で与えます。頂点番号の並びは、平面図形と同じように、表面を左に見るような向きで周回する順番に揃え、これによって面の向きが幾何学的に決まります。図形としての表面の内側に、離れ島のような、その図形に対しては穴になる領域では、頂点番号の並びは右回りに考えます。ある頂点を出発して、この多角形の辺をすべてたどって元の頂点に戻るように頂点番号の順路を考えるとき、離れ島との往復に仮の通路を考えても構いません。データは、同じ番号の頂点と、往復の通路を二度通ることになります。多角形の面積は、この多角形を三角形に分割し、三角形の面積の和として求めます。多角形の一つの辺を構成する2頂点の座標をpi,pi+1とします。任意の基準点p0を決めて、三つの点を結ぶ空間の三角形を考えます。この三角形の面積の計算は次のようにベクトル積で求めます。
ベクトル積は、一つの頂点を回転中心として、一つの辺からもう一つの辺に向かって左回りに回る向きで定義し、得られるベクトルの向きは辺に垂直で手前側になります。
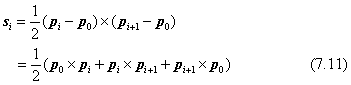
ベクトルsiは、頂点番号0, i, i+1で構成する空間の三角形に垂直な向きで、大きさは三角形の面積になります。ベクトルの向きは、頂点番号の並びの順を右回りとした右ねじの進む向き(右手系)です。多角形を構成する辺をすべてたどって、ベクトルsiの総和を求めれば、このベクトルの大きさが多角形の面積になり、向きは表面に垂直になります。この計算では、基準点p0の位置がどこにあっても無関係になります。ただし、数値計算の誤差を小さくしたいときは、多角形の重心に近いところに選ぶのがよいでしょう。体積や二次モーメントを計算する場合には、基準点をこの表面と同じ平面内に選びます。
体積の計算をする場合、適当な別の中心、例えば世界座標の原点を頂点とし、多面体の多角形を底面図形とするような多角錐を考えます。全体の多角錐の体積を総和すれば、多面体の体積になります。このとき、上で計算した多角形表面の面積、面に垂直な法線ベクトルが必要になります。多角錐の体積計算は、初等幾何で公式になっている、底面積×高さ÷6です。ただし、頂点の位置がこの表面に対して裏の位置にあるときに正の、表にあるときに負の符号を付けて体積の総和を計算します。多面体の重心、二次モーメントが必要になるときは、多面体の多角形表面を三角形に分割して考え、この三角形と原点とで作る四面体について、体積・重心・二次モーメントを計算します。この四面体の幾何学定数を加算して、全体の多面体の幾何定数を求めます。四面体の幾何定数の計算式がここで必要になります。プログラムパッケージのGEOMAPでは、ここで解説した方法で多面体モデルの幾何定数を具体的に計算するコマンドを準備しました。
次のページ