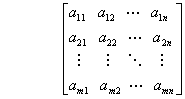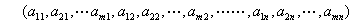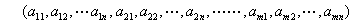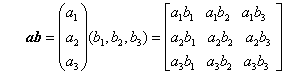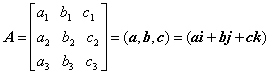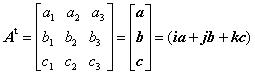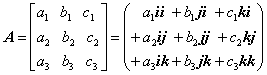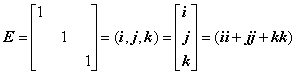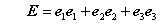A.2 量の表記法
前のページ;
次のページ
- (1) ベクトル(vector):
- n個の数をひとまとめの量として扱うときの表し方の一つがベクトルである。数の個々を成分といい、順番の番号をつけてai(i=1, … ,n)のように表す。成分全体を表すとき、(a1,a2, … ,an)のように表す。この全体を一つの数学量と定め、n次のベクトルという。成分の区切りにはカンマを入れる。表記を短くするため、このベクトルを(ai)とし、さらに記号aで代表させa=(ai)とも書く。ベクトルは幾何学において座標を表すときに利用する重要な数学量である。力学において力や運動などを表すとき、方向と大きさを持った量を表す用語として使われる。代数学的な計算において一次元の数の並びも、擬似的なn次元の空間を考えてベクトルで扱う。英字記号の使い方に大体の習慣があって、単位記号は次のようである。

- (2) 行列(matrix):
- m×n個の成分aij(i=1, … ,m ; j=1, … ,n)を、次のように並べる。これをm×n行列という。このとき、成分の区切りにカンマを使わない。
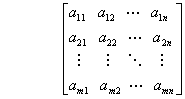
表記を短くするために、この行列を(aij)とし、さらに記号Aで代表させA=(aij)とも書く。なるべく、行列は正方行列(m=n)の形で扱うのがよい。コンピュータ言語では、行列を2次元配列として扱うことができるが、記憶領域での並びは1次元配列である。FORTRAN言語では、
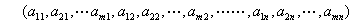
の順である。これは行列の列(縦)ベクトルを順に並べたものになる。一方、C言語では2次元配列の並びの順は行(横)ベクトルの順になることに注意する。すなわち、下の順である。
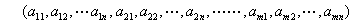
- (3)二項積(dyad)とその一次形式:
- 二つのベクトル a=(a1,a2,a3),b=(b1,b2,b3)の積で作られる次の行列を二項積といい、記号には二つのベクトルを並べて書く。
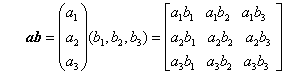
一般の行列は、列ベクトルの集合と見る。例えば、三つのベクトルをa=(a1,a2,a3),b=(b1,b2,b3),c=(c1,c2,c3)として;
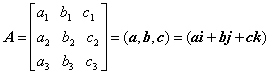
または行ベクトルの集合と見ることもある。行列Aの転置行列をAtとすると、転置行列は上のベクトル成分を行ベクトルとする行列になる。
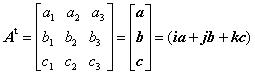
上の二つの式の右辺は、単位ベクトルとで構成した二項積の一次形式で表してある。再び、行列Aの成分に注目すると、行列は単位ベクトルを使った二項積の一次形式で与えられる。
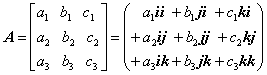
行列の各成分をテンソルと呼ぶことがあるが、上の式で示したように二つの座標軸の性質を持つ数学量であることが分かる。
- (4) 単位行列(unit matrix):
- 単位行列はEと表記する。これは、主対角線成分がすべて1、残りの成分がすべて0 である。
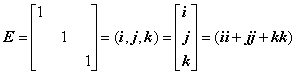
特に、最後の右辺で表した二項積の一次形式は重要な表現方法である。いま、任意の単位ベクトルの組
があって、互いに直交していれば、単位行列は次のように表すことができる。
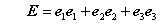
次のページ