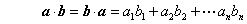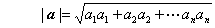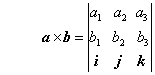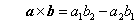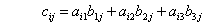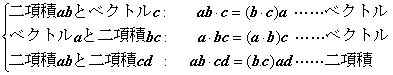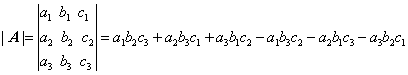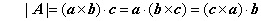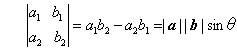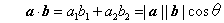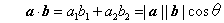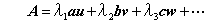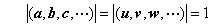A.3 演算の約束
前のページ;
目次のページ
- (1)
- 二つのベクトルa=(ai),b=(bi)の和、もしくは差(a±b)は、同じ次元のベクトルどうしについてのみ定義され、それぞれの成分の和もしくは差を成分とするベクトル(ai±bi)である。
- (2)
- ベクトルa=(ai)のスカラー倍αaとは、すべての成分をスカラー倍した成分を持ったベクトル(αai)である。
- (3)
- 二つのベクトルa=(ai),b=(bi)の積は、内積(inner product、スカラー積ともいう)のみとし、同じ次元数nのベクトルどうしについてのみ定義する。二項積(dyad)や、ベクトル積と区別するため、演算記号に・(ドット)を用いる。
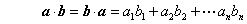
- (4)
- ベクトルa=(ai)のノルム(norm)とは、幾何学的にはベクトルの長さであって、ベクトルの記号に絶対値記号をつけて表す。
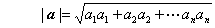
- (5)
- 二つの3次元のベトルa=(a1,a2,a3),b=(b1,b2,b3)が幾何学的なベクトルとして定義されていて、なおかつその座標系が右手系の直交座標系である場合に限って、ベクトルの外積(exterior product)、ベクトル積ともいう)が定義され、それをa×bで表す。掛け算記号を用いるのは、演算記号なしで定義した二項積(dyad)の表記と、スカラー積の表記と区別するためである。外積はベクトルとして得られ、次の行列式で求める(演算の約束は行列式参照)。
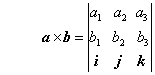
ただし、演算は、a×b=-b×aとなって、交換則は成り立たない。
- (6)
- 二つの2次元のベクトルa=(a1,a2),b=(b1,b2)
の外積は、3次元ベクトルの外積の特殊な場合であり、次のようなスカラーで定義する。
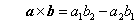
- (7)
- 二つの行列A=(aij),B=(bij)の和または差A±Bは、同じ行数、列数の行列どうしについてのみ定義され、それぞれの成分の和、もしくは差を成分とする行列(aij±bij)である。これは(m×n)個の成分をもったベクトルの和もしくは差の演算と同じである。
- (8)
- 行列A=(aij)のスカラー倍αAは、成分をスカラー倍したαaijを成分とする行列である。演算は(m×n)個の成分を持ったベクトルのスカラー倍の演算と同じである。
- (9)
- 二つの行列A=(aij),B=(bij)の積は、ABと表記するが、積の演算であることを明示的に表すためにA×Bとも表す。この場合の×記号は外積を意味しない。二つの行列の積は同じく行列であって、それをC=(cik)とする。行列Cのi行k列の成分はAのi行の横ベクトルと、Bのk列の縦ベクトルとの内積である。したがって、行列Aの列数と、行列Bの行数とは同じjでなければならない。行列AとBとが同じ3×3行列の場合、行列Cのi行j列の成分cijは次のように計算される。
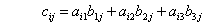
- (10)
- ベクトルと二項積との積、ならびに二つの二項積どうしの積は、ベクトル記号の接する二つのベクトルの内積を行う。残ったベクトルによって、結果がベクトルもしくは二項積となる。ただし、内積によって計算された値で全体がスカラー倍される。
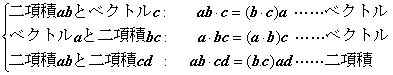
- (11)
- 行列と行列との積、ならびに行列と二項積との積は、基本的には互いに接するベクトル間でのスカラー積で行われる。例えばM×abの場合には、行列Mは行ベクトルの集合とした二項積の表現方法を使って演算する。行列Mと単独のベクトルaとの積M×aまたはa×Mでは、ベクトルaは、単位ベクトルiとの二項積aiもしくはiaと考えることができる。
- (12)
- 3×3の行列A=(a,b,c)の行列式(determinant)は、行列記号に絶対値記号||をつけて表し、3次の行列においては、次のように計算される。
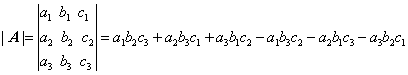
もしくは、
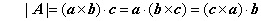
3次の行列式は、幾何学的にいえば、平行六面体の三本の稜線が三つのベクトルa,b,cであるときの、平行六面体の体積に等しい。ただし、符号は、a,b,cが右手系の位置関係にあるときに正、そうでないとき負である。
- (13)
- 二つの2次元のベクトルa=(a1,a2),b=(b1,b2)で構成する2次元の行列A=(a,b)の行列式(determinant)は、二つのベクトルa,bの長さとそのベクトルの交わる角度θを使って、
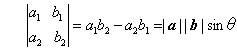
ただしθは、ベクトルaからベクトルbに向かって反時計回りに回転させて測る角度である。なお、ベクトルa,bの内積は次のように表される。
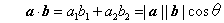
- (14)
- 一般的なn次の行列の行列式の値は、実用的な数値計算においてほとんど必要としない。しかし、行列が下のように二項積の一次形式で表されているときは、固有値の積で行列式が与えられる。説明のため、3次の行列の場合を示そう。ここで、(a,b,c,…),(u,v,w,…)は、それぞれ互いに直交する右手系の単位ベクトルを構成していてλ1、λ2、λ3、…は固有値である。
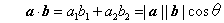
一般的に>n>3の場合には右手系という定義の代わりに、次のような条件が必要である。
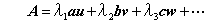
行列式は次のようになる。
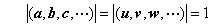
次の章のページ