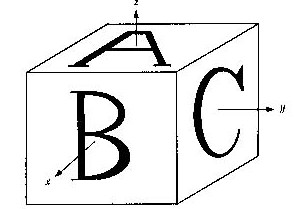
下の見取り図と展開図とに示すように、各面を識別するために英字のAからFまでを書き込んだ立方体(正六面体)が机の上に置いてある状態を考える。立方体を世界座標の原点に置いた基準状態が見取り図に示してある。面B、C、Aの各面は、座標軸x、y、z軸の正の向きを向いている。この立方体を回転させて向きを変えて置く置き方は24通りある。この回転を与える行列を表にまとめた。
図C.1 基準状態での座標系

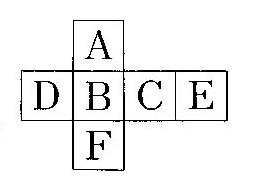
図C.2 展開図と各面の文字の関係
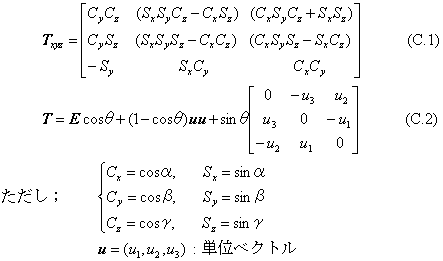
|
|
1 |
2 |
3 |
4 |
||||||||
B |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | 0 | -1 |
0 | -1 | 0 |
0 | 0 | 1 |
|
0 | 0 | 1 |
0 | 1 | 0 |
0 | 0 | -1 |
0 | -1 | 0 |
|
C |
0 | 1 | 0 |
0 | 1 | 0 |
0 | 1 | 0 |
0 | 1 | 0 |
-1 | 0 | 0 |
0 | 0 | -1 |
1 | 0 | 0 |
0 | 0 | 1 |
|
0 | 0 | 1 |
-1 | 0 | 0 |
0 | 0 | -1 |
1 | 0 | 0 |
|
D |
0 | -1 | 0 |
0 | -1 | 0 |
0 | -1 | 0 |
0 | -1 | 0 |
1 | 0 | 0 |
0 | 0 | -1 |
-1 | 0 | 0 |
0 | 0 | 1 |
|
0 | 0 | 1 |
1 | 0 | 0 |
0 | 0 | -1 |
-1 | 0 | 0 |
|
E |
-1 | 0 | 0 |
-1 | 0 | 0 |
-1 | 0 | 0 |
-1 | 0 | 0 |
0 | -1 | 0 |
0 | 0 | -1 |
0 | 1 | 0 |
0 | 0 | 1 |
|
0 | 0 | 1 |
0 | -1 | 0 |
0 | 0 | -1 |
0 | 1 | 0 |
|
A |
0 | 0 | 1 |
0 | 0 | 1 |
0 | 0 | 1 |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
0 | 1 | 0 |
0 | -1 | 0 |
|
-1 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
0 | -1 | 0 |
|
F |
0 | 0 | -1 |
0 | 0 | -1 |
0 | 0 | -1 |
0 | 0 | -1 |
0 | 1 | 0 |
-1 | 0 | 0 |
0 | -1 | 0 |
1 | 0 | 0 |
|
1 | 0 | 0 |
0 | 1 | 0 |
-1 | 0 | 0 |
0 | -1 | 0 |
|
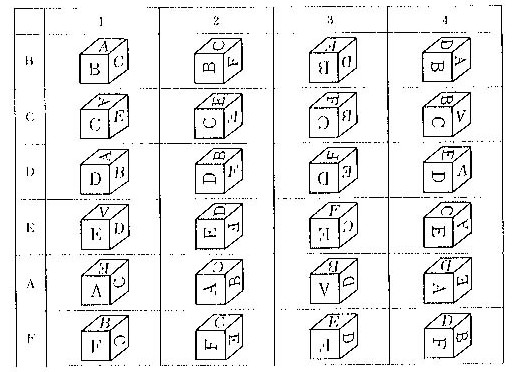
図C.3 位置決めの見取り図
回転軸の向きを表す |
軸回転角 |
オイラー回転角 |
向きコード | ||
α |
β |
γ |
|||
x軸 |
90 |
90 |
0 |
0 |
B2 |
180 |
180 |
0 |
0 |
B3 |
|
-90 |
-90 |
0 |
0 |
B4 |
|
y軸 |
90 |
0 |
90 |
0 |
A1 |
180 |
0 |
180 |
0 |
E3 |
|
-90 |
0 |
-90 |
0 |
F1 |
|
z軸 |
90 |
0 |
0 |
90 |
D1 |
180 |
0 |
0 |
180 |
E1 |
|
-90 |
0 |
0 |
-90 |
C1 |
|
u=(1,1,0)/√2 |
180 |
180 |
0 |
90 |
C3 |
u=(1,-1,0)/√2 |
180 |
180 |
0 |
-90 |
D3 |
u=(1,0,1)/√2 |
180 |
0 |
-90 |
180 |
A3 |
u=(1,0,-1)/√2 |
180 |
0 |
90 |
180 |
F3 |
u=(0,1,1)/√2 |
180 |
-90 |
180 |
0 |
E4 |
u=(0,1,-1)/√2 |
180 |
90 |
180 |
0 |
E2 |
u=(1,1,1)/√3 |
120 |
90 |
0 |
90 |
A2 |
-120 |
0 |
-90 |
-90 |
C4 |
|
u=(-1,1,1)/√3 |
120 |
0 |
90 |
90 |
D4 |
-120 |
90 |
0 |
-90 |
F2 |
|
u=(-1,-1,1)/√3 |
120 |
-90 |
0 |
90 |
F4 |
-120 |
90 |
90 |
0 |
C2 |
|
u=(1,-1,1)/√3 |
120 |
90 |
-90 |
0 |
D2 |
-120 |
-90 |
0 |
-90 |
A4 |
|