附録D　アフィン変換の計算式

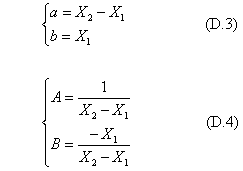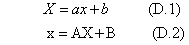
　図形の移動・回転・変形をさせるアフィン変換の実用計算式を要約して示す。実践的な考え方として、単位寸法の領域に描かれた図形の座標の一組を別の図形の座標の一組に対応させる変換とその逆変換との計算式をまとめた。

D.1　一次元のアフィン変換

　下の式(D.1)で示す一次方程式とその逆変換式(D.2)との関係を、与えられた二つの点との対応関係を満たす条件で係数を定める計算式を示す。変数Xをyに変えれば、式そのものは初歩的な一次式y=ax+bである。ここでは、後で説明する二次元（平面図形）と、三次元（立体図形）のアフィン変換と射影変換の式と対比させるために付した。

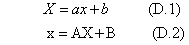
　二組の係数(a,b),(A,B)を定めるため、x座標上の二点は原点(0)と単位点(1)とし、X座標上の二点(X₁,X₂)を次のように対応させる。

係数の値は下のように得られる