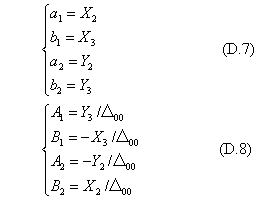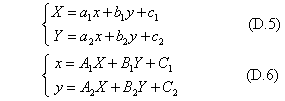
二次元のアフィン変換は、二つの平行四辺形が与えられていて、一方の四辺形を相手側に嵌め込むように移動・回転・変形をさせることである。数学的には、一方の三角形を他方の三角形に重ねるように図形を変換する条件になるので、平行四辺形の3頂点の座標を考える。一方の四辺形は単位の正方形とし、その左下隅を原点に置く。任意の形状の平行四辺形同士のアフィン変換に応用するときは、変換元の四辺形の逆変換を求めて、それを変換先の四辺形に嵌め込む。変換・逆変換の代数式の一般形は次の表現である。
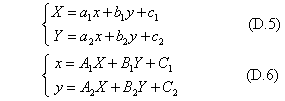
実用計算式が複雑になることを避けるため、変換先の四辺形の左下隅の頂点も原点にオフセットした状態で係数の計算式を求める。3頂点の座標は下のように対応させる。この条件では、式(D.5)と(D.6)において、c1=c2=C1=C2=0になる。
(x,y) |
⇔ |
(X,Y) |
(0,0) |
⇔ |
(0,0) |
(1,0) |
⇔ |
(X2,Y2) |
(0,1) |
⇔ |
(X3,Y3) |
図D.1 平面図形のアフィン変換
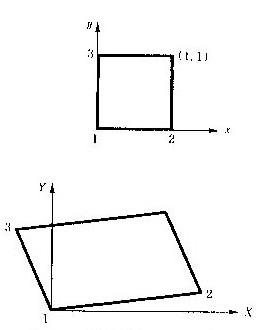
式の係数の解は式(D.7)と(D.8)である。ここで、式(D.8)で使われる係数の表式に使うため、下に示すような計算補助の中間定数を定義しておく。
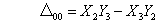
ここに、Δ00は、三角形(123)の面積の2倍を計算しているので、この値が0になってはならない。またΔ00<0の場合には裏返しの変換になる。