D.3　三次元のアフィン変換

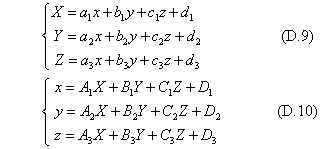
　三次元のアフィン変換は、二つの平行六面体が与えられていて、一方の六面体を相手側に嵌め込むように移動・回転・変形をさせる。数学的には、一方の四面体を他方の四面体に重ねるように図形を変換する条件になる。平行六面体8個の内の4頂点の座標を考え、一つの頂点を共通点とした3辺の頂点とする。変換元の六面体は単位の立方体とし、共通点を原点に置く。変換先の平行六面体には、対応する4頂点を考える。変換および逆変換の一般式は、(D.9)および(D.10)である。

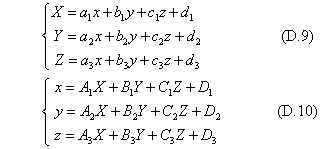
　四頂点の座標は下のように対応させる。実用計算式を簡単にするため、共通点(X₁,Y₁,Z₁)を原点にオフセットした状態で係数の算定式を示す。

　上で示した対応点の関係では、式(D.9)と(D.10)において、d₁=d₂=d₃=0およびD₁=D₂=D₃=0になる。係数の解は式(D.11)と(D.12)である。ここで、式(D.12)で使われる係数の表式に使うため、下のΔ₀₀₀に示すような中間定数を定義しておく。この値は平行六面体の体積である。通常の変換は正の値であるが、負の場合には左右が反転するような変換を伴う。

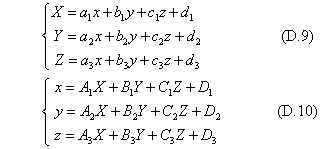
　任意の形状の平行六面体から別の平行六面体への嵌め込みの変換は、変換元の六面体を逆変換で単位の立方体に変換させ、改めて変換先の六面体への変換を行なわせればよい。