附録E　射影変換の計算式

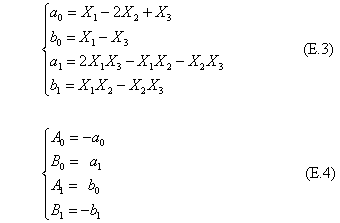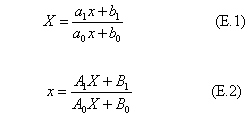
　図形の移動・回転・変形を代数式で表す変換の種類の中で、ここでは一般的な射影変換について、実用計算式をまとめた。実践的な考え方として、単位寸法の領域に描かれた図形の座標の一組を別の図形の座標の一組に対応させる変換とその逆変換との計算式をまとめた。

E.1　一次元の射影変換

　二つの直線座標軸xとX上の座標について、一次元の射影変換とその逆変換の基本式は下のような表現である。

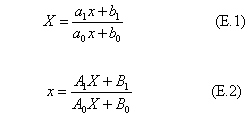
三頂点の座標は下のように対応させる。

　それぞれの軸上の三点が重なるように変換するとして式の係数を求める。なお、式(E.1)、(E.2)は分数式であるので、係数全体をスカラー倍して使うことができる。