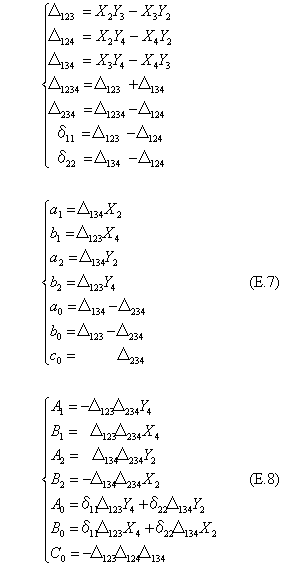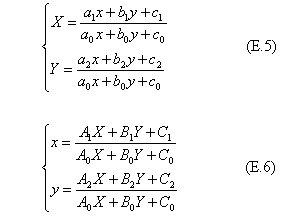
二つの四辺形それぞれの頂点が重なるように一方の四辺形を相手側に嵌め込む射影変換の係数を求める。一方の四辺形は単位の正方形とし、その左下隅を原点に置く。任意の形状の四辺形同士の射影変換に応用するときは、変換元の四辺形の逆変換を求めて、それを変換先の四辺形に嵌め込む。変換・逆変換の代数式の一般形は次の表現である。
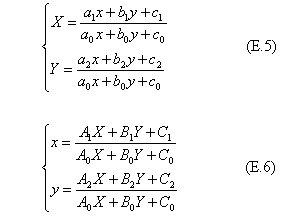
図E.1 平面図形の射影変換
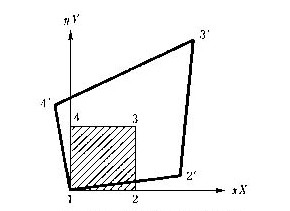
実用計算式を単純化するため、変換先の四辺形の左下隅の頂点も原点にオフセットした状態で係数の計算式を求める。4頂点の座標は下のように対応させる。この条件は、c1=c2=C1=C2=0になる。
(x,y) |
⇔ |
(X,Y) |
(0,0) |
⇔ |
(0,0) |
(1,0) |
⇔ |
(X2,Y2) |
(1,1) |
⇔ |
(X3,Y3) |
(0,1) |
⇔ |
(X4,Y4) |
式(E.7)と(E.8)で示す係数の表式を見やすくし、重複した計算を少なくするように、下に示すような中間定数を定義しておく。射影変換が成立する条件は、Δijkが0でなく、すべて同符号である。これは、四変形を構成する3頂点が同一直線上にない条件である。Δijkの符号が負であるときは、左右反転の変換が生じる。