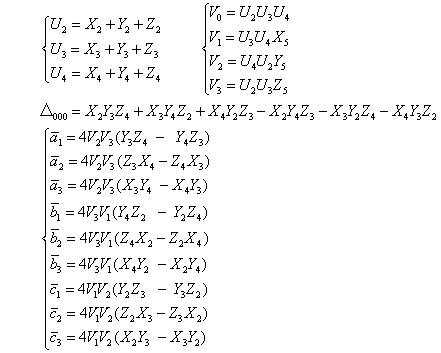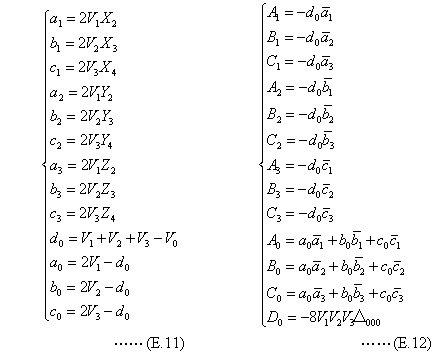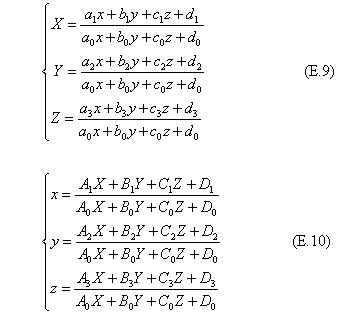
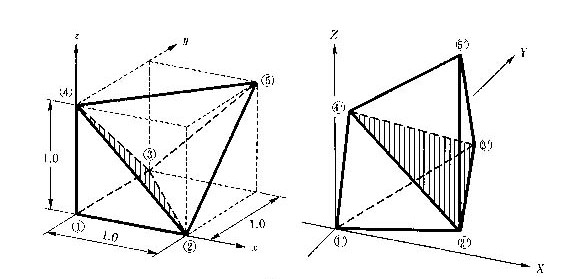
三次元の幾何モデルを射影変換させる場合、二つの四面体が底辺で接したような、各面が三角形から成る六面体を基本立体にする。この六面体は面6、辺9、頂点5である。変換は、二つの六面体が与えられていて、対応する頂点が重なるように一方の六面体を相手側に嵌め込む射影変換および、その逆向きの射影変換を求める。一方の六面体は、単位の立方体から5頂点を選び、その左下隅を原点に置く。頂点番号の対応において、(2、3、4)番の頂点で構成する三角形の面に対して、(1、5)番の頂点はそれぞれ反対側にあるとする。変換・逆変換の代数式は下記である。
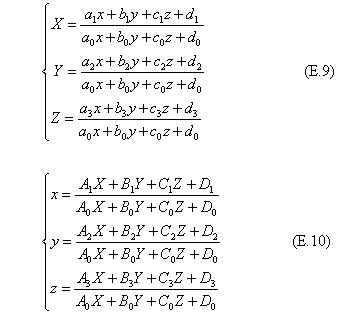
図E.2 立体図形の射影変換
実用計算式を単純化するため、変換先の六面体の左下隅の頂点も原点にオフセットした状態で係数の計算式を求める。この条件は、d1=d2=d3=0およびD1=D2=D3=0になる。5頂点の座標は下のように対応させる。
(x,y,z) |
⇔ |
(X,Y,Z) |
(0,0,0) |
⇔ |
(0,0,0) |
(1,0,0) |
⇔ |
(X2,Y2,Z2) |
(0,1,0) |
⇔ |
(X3,Y3,Z3) |
(0,0,1) |
⇔ |
(X4,Y4,Z4) |
(1,1,1) |
⇔ |
(X5,Y5,Z5) |
式(E.11)と(E.12)で示す係数の表式を見やすくし、重複した計算を少なくするように、次に示すような中間定数を定義しておく。