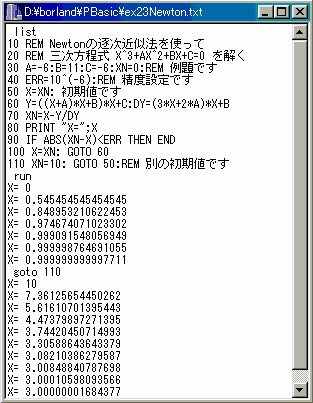
ニュートン法で、何かの関数の逆関数を求める方法の説明用に作りました。上の例題は、上と同じ三次方程式です。一般的な問題の応用には、解きたい関数本体Y、その一回微分した式dYを差し換えればよいのです。このプログラミングの場合、元の三次式を表す方法として、べき乗の演算子＾を使わないで、多重括弧を使ってY=((X+A)*X+B)*X+Cの形に変形していることに注目して下さい。Newton法では、初期値から出発して補正を繰り返して一つの解を得ます。二つ以上の解があるときは、あらかじめ、どの当たりに解があるかの初期値を入れ直さなければなりません。また、繰り返し計算を止める条件として、精度を決めておかなければなりません。もし極大または極小値があると無限ループに入る危険があります。これを避けるため、FOR-NEXT文で50回の繰り返しで計算を停止するようにしてあります。
（図2.3 ex23Newton.txt）。